Home
Class 12
PHYSICS
Two boys are standing at the ends A and ...

Two boys are standing at the ends A and B of a ground, where `AB=a`. The boy at B starts running in a direction perpendicular to AB with velocity `v_(1)`. The boy at A starts running simultaneously with velocity v and catches the other boy in a time t, where t is :

Text Solution

Verified by Experts

Let two boys meet at point C after time 't' from the starting.
Then AC=vt, BC`=v_(1)t` but `(AC)^(2)=(AB)^(2)+(BC)^(2)rArrv^(2)t^(2)=a^(2)+v_(1)^(2)t^(2)`
`rArrt^(2)(v^(2)-v_(1)^(2))=a^(2)rArrt=sqrt((a^(2))/(v^(2)-v_(1)^(2)))`
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A PALNE

    ALLEN |Exercise EXERCISE-3|41 Videos

  • KINEMATICS-2D

    ALLEN |Exercise Exercise (O-2)|47 Videos

  • NEWTON'S LAWS OF MOTION & FRICTION

    ALLEN |Exercise EXERCISE (JA)|4 Videos

Similar Questions

Explore conceptually related problems

A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement. The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as L_(x) , and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity V_(x) and of widht D and he is swimming in direction perpendicular to the river flow with velocity V_(y) relation to river, assuming no use of directed lengths, the quantities of interest are then V_(x),V_(y) both dimensioned as (L)/(T) , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S prop V_(x)^(a)V_(y)^(b)D^(c) Or dimensionally L=((L)/(T))^(a+b)xx(L)^(c) from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then V_(x) will be dimensioned as (L_(x))/(T), V_(y) as (L_(y))/(T), S as L_(x)" and " D as L_(y) . The dimensional equation becomes : L_(x)=((L_(x))/(T))^(a) ((L_(y))/(T))^(b)(L_(y))^(c) and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent. A conveyer belt of width D is moving along x-axis with velocity V. A man moving with velocity U on the belt in the direction perpedicular to the belt's velocity with respect to belt want to cross the belt. The correct expression for the drift (S) suffered by man is given by (k is numerical costant )

A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement. The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as L_(x) , and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity V_(x) and of widht D and he is swimming in direction perpendicular to the river flow with velocity V_(y) relation to river, assuming no use of directed lengths, the quantities of interest are then V_(x),V_(y) both dimensioned as (L)/(T) , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S prop V_(x)^(a)V_(y)^(b)D^(c) Or dimensionally L=((L)/(T))^(a+b)xx(L)^(c) from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then V_(x) will be dimensioned as (L_(x))/(T), V_(y) as (L_(y))/(T), S as L_(x)" and " D as L_(y) . The dimensional equation becomes : L_(x)=((L_(x))/(T))^(a) ((L_(y))/(T))^(b)(L_(y))^(c) and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent. From the concept of directed dimension what is the formula for a range (R) of a cannon ball when it is fired with vertical velocity component V_(y) and a horizontal velocity component V_(x) , assuming it is fired on a flat surface. [Range also depends upon acceleration due to gravity , g and k is numerical constant]

Two cars A and B are at positions 50 m and 100 m from the origin at t = 0. They start simultaneously with constant velocities 10 m/s and 5 m/s respectively in the same direction. Find the time at which they will overtake one another.

A trolley was moving horizontally on a smooth ground with velocity v with respect to the earth. Suddenly a man starts running from rear end of the trolley with a velocity (3//2)v with respect to the trolley. After reaching the other end, the man turns back and continues running with a velocity (3//2)v with respect to trolley in opposite direction. If the length of the trolley is L, find the displacement of the man with respect to earth when he reaches the starting point on the trolley. Mass of the trolley is equal to the mass of the man.

A trolley is moving horizontally with a constant velocty of v m//s w.e.t. earth. A man starts running from one end of the trolley with velocity 1.5v m//s w.r.t. to trolley. After reaching the opposite end, the man return back and continues running with a velocity of 1.5 v m//s w.r.t. the trolley in the baclward direction. If the length of the trolley is L then the displacement of the man with respect to earth during the process will be :-

Two objects move in the same direction in a straight line. One moves with a constant velocity v_(1) . The other starts at rest and has constant acceleration a. They collide when the second object has velocity 2v_(1) . The distance between the two objects when the second one starts moving is :-

One U shaped conducting frame is placed in a plane perpendicular to uniform magnetic field B. One conducting rod of mass m and length l is kept perpendicular to parallel sides of this frame. At time t = 0, this rod is pushed perpendicular to its length with initial velocity v_g . Prove that its velocity at the end of time t is v_t=v_0 "exp" ((-B^2l^2)/(mR)t) where R=resistance of external circuit and l=perpendicular distance between two parallel slides .

A U-shaped conducting frame is placed in a magnetic field B in such a way that the plane of the frame is perpendicular to the field lines. A conducting rod is supported on the parallel arms of the frame, perpendicular to them and is given a velocity v_0 at time t = 0. Prove that the velocity of the rod at time t will be given by v_t=v_0 "exp" ((-B^2l^2)/(mR)t) .

When you are standstill holding a flag, the flag flutters in the direction of wind. When you start running the direction of fluttering of the flag changes to the direction of the wind relative to you. In all case a flag flutters in the direction of the wind relative to the flag. Winds is blowing uniformly due north everywhere with velocity 12 m/s. A car mounted with a flag starts running towards cast. after 9s from starts the flag flutters in 53^(@) north of west and after 16 s from the start the flag flutters in 37^(@) north of west. (a) Find velocity of the car 9 s after it starts. (b) Find velocity of the car 16 s after it starts. (c) If the car maintains uniform acceleration, find acceleration of the car.

The velocity of a particle moving in the positive direction of the x axis varies as v=alphasqrtx , where alpha is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0 , find: (a) the time dependence of the velocity and the acceleration of the particle, (b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.

ALLEN -MOTION IN A PALNE-SOLVED EXAMPLE
  1. Two bodies are thrown with the same initial speed at angles alpha and ...

    Text Solution

    |

  2. The range of a projectile launched at an angle of 15^(@) with horizont...

    Text Solution

    |

  3. A ball of mass (m) is thrown vertically up. Another ball of mass 2 m ...

    Text Solution

    |

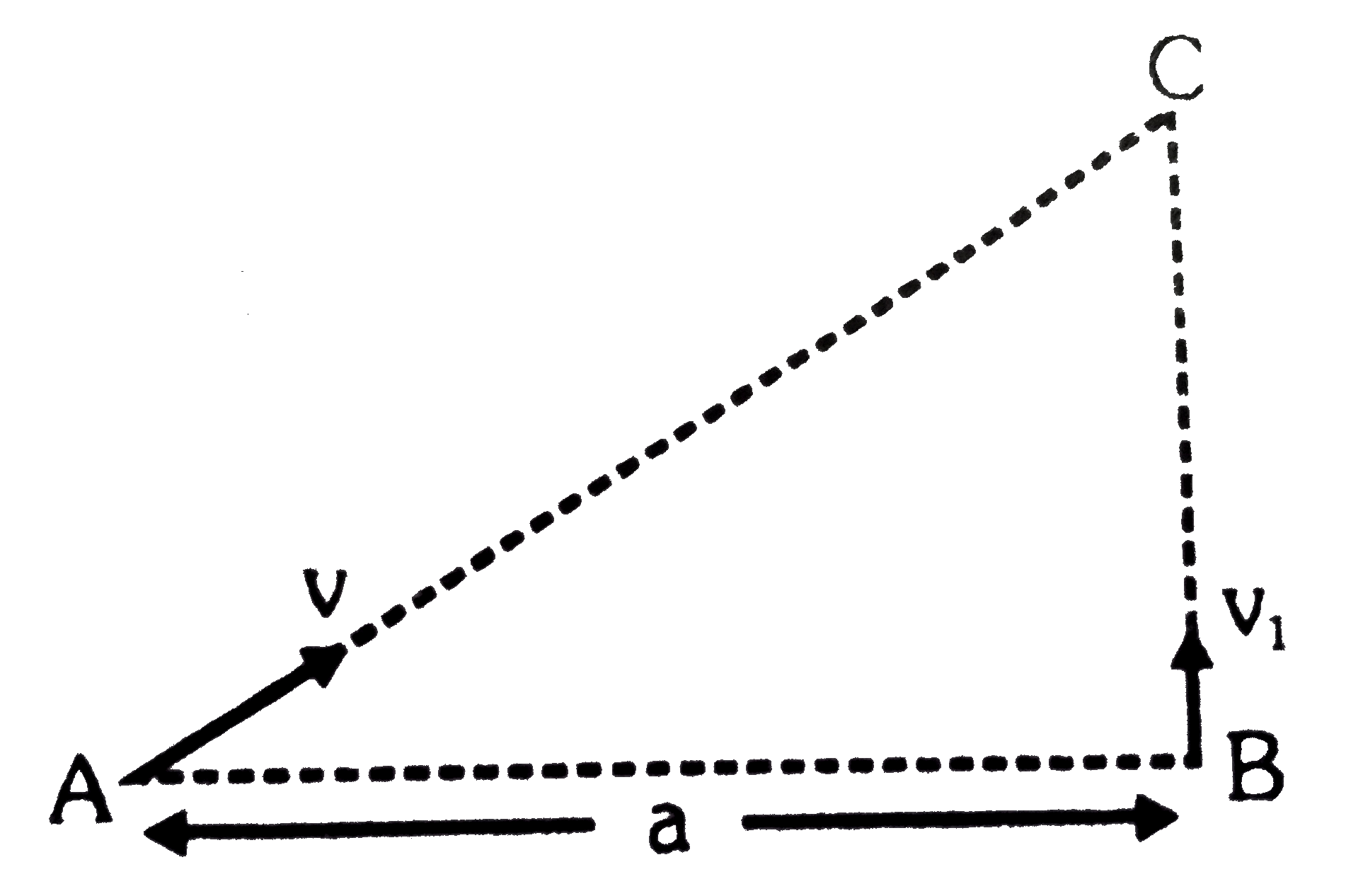
  4. A body is projectd with the velcity (U1) from the point (A) as shown...

    Text Solution

    |

  5. An aeroplane is flying at a constant height of 1960 m with speed 600 k...

    Text Solution

    |

  6. A body is projected up such that its position vector varies with time ...

    Text Solution

    |

  7. Two particles A and B are projected simultaneously in the directins sh...

    Text Solution

    |

  8. Two bodies were thrown simultaneously from the same point, one straigh...

    Text Solution

    |

  9. Two particles are projected from the two towers simultaneously, as sho...

    Text Solution

    |

  10. A projectile is thrown with speed u making angle theta with horizontal...

    Text Solution

    |

  11. A particle has initial velocity (3hati+4hatj) and has acceleration (0....

    Text Solution

    |

  12. A particle travels according to the equation y=x-(x^(2)/(2)). Find the...

    Text Solution

    |

  13. A stone is to be thrown so as to cover a horizontal distance f 3m. If ...

    Text Solution

    |

  14. Two projectiles are projected at angles ( theta) and ((pi)/(2) - theta...

    Text Solution

    |

  15. Two boys are standing at the ends A and B of a ground, where AB=a. The...

    Text Solution

    |

  16. Show that projection angle theta(0) for a projectile launched from the...

    Text Solution

    |

  17. A body stans at 78.4 m from a building and throws a ball which just en...

    Text Solution

    |

  18. A particle starts from origin at t=0 with velocity 5.0hati m//s and mo...

    Text Solution

    |

  19. A particle is projected from the ground at an angle such that it just ...

    Text Solution

    |

  20. An aeroplane is travelling at a height of 2000 m from the ground. The ...

    Text Solution

    |