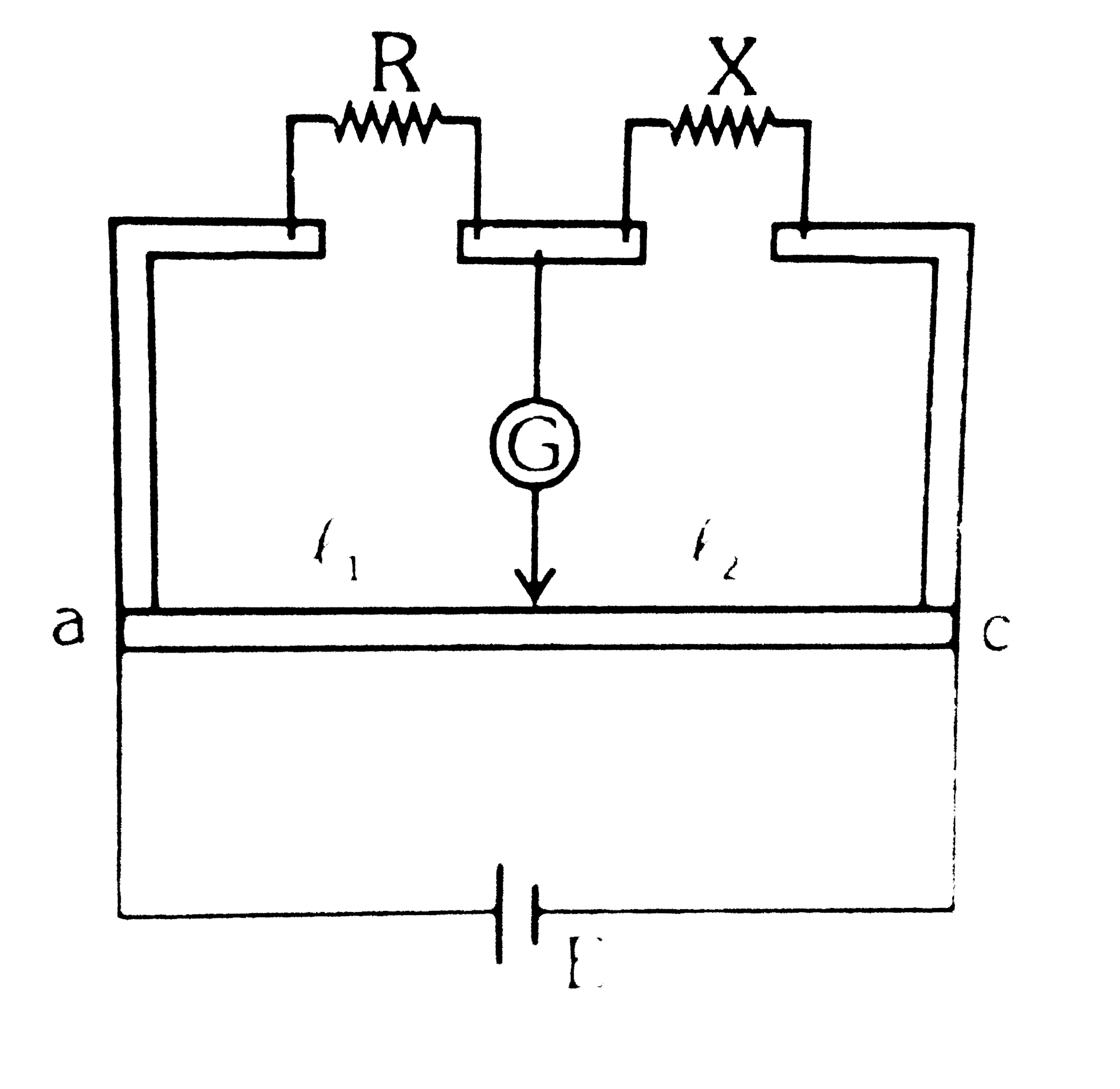
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Practical diagram for meter bridge is as shown in figure. (a) G defl...
Text Solution
|
- When two known resistance R and S are connected in the left and right ...
Text Solution
|
- In the figure shown PQ is a potentiometer wire. When galvanometer is c...
Text Solution
|
- Figure (a) below shows a wheat stone bridge in which P, Q, R, S are fi...
Text Solution
|
- The Wheatstone bridge shown in the above figure is balanced. If the po...
Text Solution
|
- दर्शाए गए चित्र में मीटर ब्रिज के तार की लम्बाई 80 सेमी है । जब A...
Text Solution
|
- निम्न चित्र में प्रदर्शित मीटर सेतु में शून्य विक्षेप कि स्थिति 6...
Text Solution
|
- चित्र में दर्शाए परिपथ में धारामापी G शून्य विक्षेप दर्शाता है। यदि बै...
Text Solution
|
- नीचे दिए गए चित्र में गैल्वैनोमीटर में शून्य विक्षेप के साथ मीटर सेतु ...
Text Solution
|