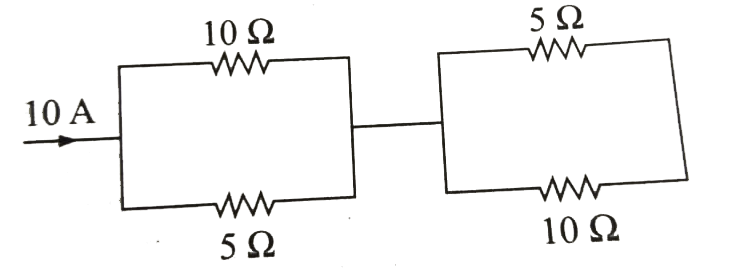
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Four resistances carrying a current shown in Fig. 7.41 are immersed in...
Text Solution
|
- Four resistances carrying a current shown in Fig. 7.41 are immersed in...
Text Solution
|
- The entropy change in melting 1g of ice at 0^@C . (Latent heat of ice ...
Text Solution
|
- Consider the following arrangement of resistors . This arrangement is ...
Text Solution
|
- If we keep a box of ice creasm in a freezer for too long, crystals of ...
Text Solution
|
- बर्फ के गलन की गुप्त ऊष्मा 80 कैलोरी/ग्राम है। 0^@C की 500 ग्राम बर्फ...
Text Solution
|
- 1 किग्रा बर्फ का ताप -5^@C है। सम्पूर्ण बर्फ का पिघलाने के लिए इसे कि...
Text Solution
|
- एक बॉक्स का क्षेत्रफल 5000 cm^2 तथा इसकी दीवार की मोटाई 6 मिमी है। इ...
Text Solution
|
- खाने की वस्तुओ को ठंडा रखने के लिए प्रयुक्त बर्फ बॉक्स की दीवारों का ...
Text Solution
|