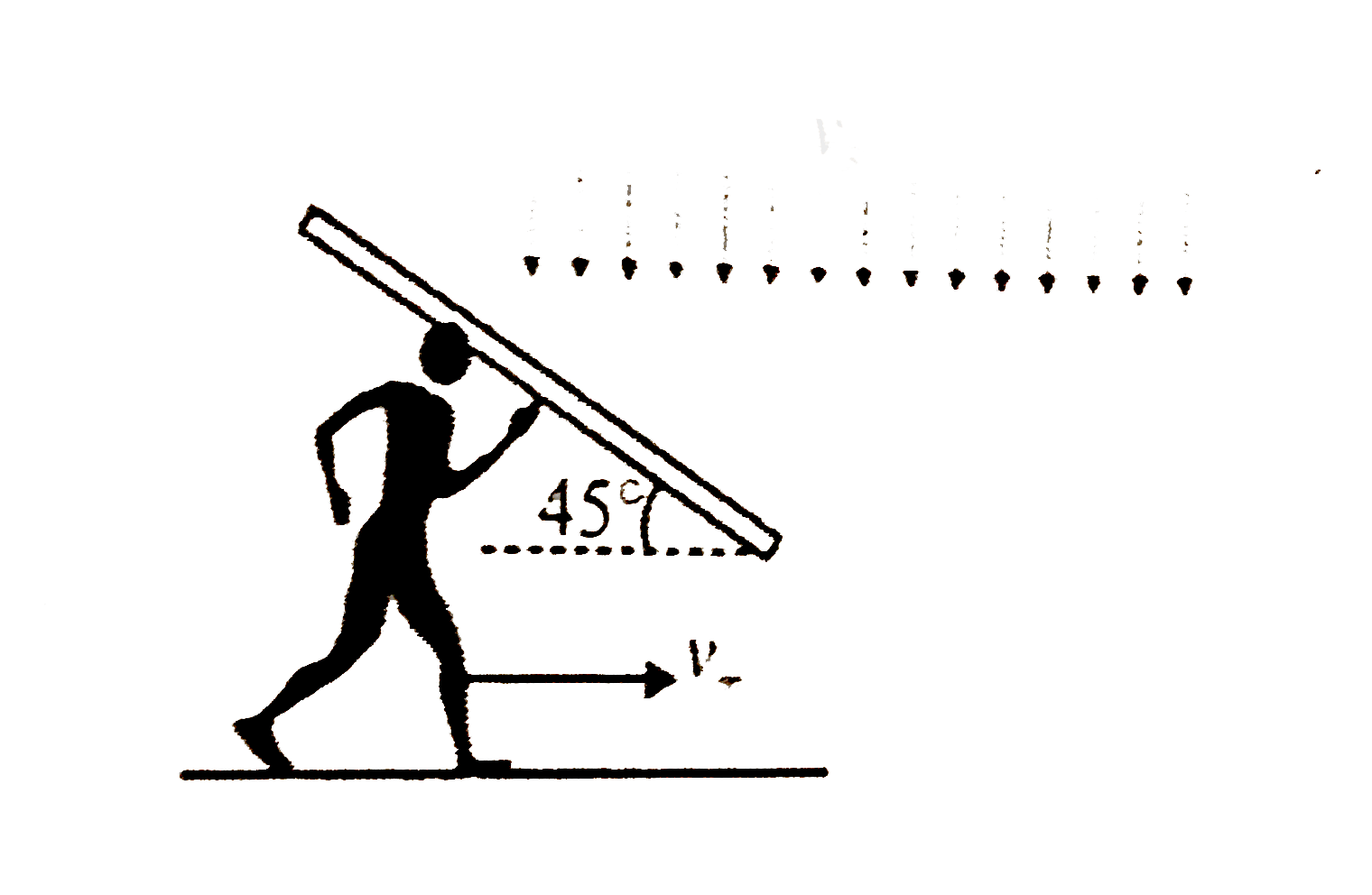Home
Class 12
PHYSICS
On a particular day rain drops are falli...

On a particular day rain drops are falling vertically at a speed of 5 m/s. A man holdind a plastic board is running to escape from rain as shown. The lower end of board is at a height half that of man and the board makes `45^(@)` with horizontal. The maximum speed of man so that his feet does not get wet, is

A

5 m/s

B

`5sqrt()2` m/s

C

`5//sqrt()2` m/s

D

zero

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS-2D

    ALLEN |Exercise Exercise (O-1)|40 Videos

  • GRAVITATION

    ALLEN |Exercise EXERCISE 4|9 Videos

  • MOTION IN A PALNE

    ALLEN |Exercise SOLVED EXAMPLE|28 Videos

Similar Questions

Explore conceptually related problems

Rain is falling vertically with a speed of 20ms^(-1) ., A person is running in the rain with a velocity of 5 ms^(-1) and a wind is also blowing with a speed of 15 ms^(-1) (both from the west) The angle with the vertical at which the person should hold his umbrella so that he may not get drenched is:

A man is moving due east with a speed 1 km/hr and rain is falling vertically with a speed sqrt(3) km/hr. At what angle from vertical the man has to hold his umbrella to keep the rain away. Also find the speed of rain drops w.r.t. man.

By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation. vec(v)_(rm)=vec(v)_(r)-vec(v)_(m) A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure. When you are standstill in rain, you have to hold umbrella vertically to protect yourself. (a) When you walk with velocity 90 cm/s, you have to hold your umbrella at 53^(@) above the horizontal. What is velocity of the raindrops relative to the ground and relative to you ? (b) If you walk with speed 160 cm/s, how should you hold your umbrella ?

By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation. vec(v)_(rm)=vec(v)_(r)-vec(v)_(m) A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure. Rain is falling vertically with velocity 80 cm/s. (a) How should you hold your umbrella ? (b) You start walking towards the east with velocity 60 cm/s. How should you hold umbrella ? (c) You are walking towards the west with velocity 60 cm/s. How should you hold your umbrella ? (d) You are walking towards the north with velocity 60 cm/s. How should you hold your umbrella? (e) You are walking towards the south with velocity 80 cm/s. How should you hold your umbrella ?

A man standing on a road has to hold his umbrella at 30^(@) with the vertical to keep the rain away. He throws the umbrella and starts running at 10km/hr. He finds that rain drop are hitting his head vertically. Find the speed of rain drops with respect to (a) road (b) the moving man.

A man runs across the roof, top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is at a lower height than the first. If his speed is 9 m/s. the horizontal) distance between the two buildings is 10 m and the height difference is 9 m, will be able to land on the next building? (Take g = 10 m//s^(-2) )

A man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle theta to the vertical. The velocity of rain with respect to the ground is :

A trolley is moving horizontally with a constant velocty of v m//s w.e.t. earth. A man starts running from one end of the trolley with velocity 1.5v m//s w.r.t. to trolley. After reaching the opposite end, the man return back and continues running with a velocity of 1.5 v m//s w.r.t. the trolley in the baclward direction. If the length of the trolley is L then the displacement of the man with respect to earth during the process will be :-

A man walking briskly in rain with speed v must slant his umbrella forward making an angle theta with the vertical. A student derives the following relation between theta and v: tan theta = v and checks that the relation has a correct limit : as vtoo, thetato0 , as expected , (we are assuming there is no strong wind and that the rain falls vertically for a stationary man.) Do you think this relation can be correct ? If you, guess the correct relation.

A rain drop of radius 2 mm falls from a height of 500 m above the ground .It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height , it attains its maximum (terminal) speed, and moves with uniform speed thereafter .What is the work done by the gravitational force on the drop in the first and second half of its journey ?What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 1 ms^(-1) ?

ALLEN -KINEMATICS-2D-Exercise (O-2)
  1. An object moves to the East across a frictionless surface with constan...

    Text Solution

    |

  2. A particle is thrown from a stationary platform with velocity v at an ...

    Text Solution

    |

  3. On a particular day rain drops are falling vertically at a speed of 5 ...

    Text Solution

    |

  4. A 2-m wide truck is moving with a uniform speed v(0)=8 m/s along a str...

    Text Solution

    |

  5. Man A is sitting in a car moving with a speed of 54 (km)/(hr) observes...

    Text Solution

    |

  6. A swimmer swins in still water at a speed =5 km//hr. He enters a 200m ...

    Text Solution

    |

  7. A man wishes to swim across a river 40 m wide flowing with a speed of ...

    Text Solution

    |

  8. An observer on ground sees a boat cross a river of width 800 m perpend...

    Text Solution

    |

  9. A boatman moves his boat with a velocity 'v' (relative to water) in ri...

    Text Solution

    |

  10. A ball is thrown at an angle theta up to the top of a cliff of height ...

    Text Solution

    |

  11. A projectile of mass 1kg is projected with a velocity of sqrt(20)m//s ...

    Text Solution

    |

  12. A particle is moving with a position vector, vec(r)=[a(0) sin (2pi t) ...

    Text Solution

    |

  13. A point mass is moving in the x-y plane. Its acceleration is a constan...

    Text Solution

    |

  14. A ball is thrown from ground such that it just crosses two poles of eq...

    Text Solution

    |

  15. Position vector of a particle is expressed as function of time by equa...

    Text Solution

    |

  16. A projectile is thrown with speed u into air from a point on the horiz...

    Text Solution

    |

  17. A block is thrown with a velocity of 2m//s^(-1) (relative to ground) o...

    Text Solution

    |

  18. A man on a rectilinearly moving cart, facing the direction of motion, ...

    Text Solution

    |

  19. A cubical box dimension L = 5//4 m starts moving with an acceleration ...

    Text Solution

    |

  20. A large rectangular box moves vertically downward with an acceleration...

    Text Solution

    |