Home
Class 11
PHYSICS
A vector vecA and vecB make angles of 20...

A vector `vecA` and `vecB` make angles of `20^(@)` and `110^(@)` respectively with the X-axis. The magnitudes of these vectors are 5m and 12 m respectively. Find their resultant vector.

Text Solution

Verified by Experts

Angle between the `vecA and vecB = 110^(@) - 20^(@) = 90^(@)`
So `R= sqrt(A^(2) + B^(2)+ 2AB cos 90^(@))= sqrt(5^(2) 12^(2))= 13m `
Let angle of `vecR` from `vecA` is `alpha`
`tanalpha = (Bsintheta )/(A+B sin theta)= (12sin 90^(@))/(5+12 cos 90^(@))= (12xx1)/(5+12xx0) = (12)/(5)`
`rArr alpha = tan^(-1) ((12)/(5))` with vector `vecA or (alpha + 20^(@))` with X-axis.
Promotional Banner

Topper's Solved these Questions

  • BASIC MATHEMATICS USED IN PHYSICS &VECTORS

    ALLEN |Exercise BEGINNER S BOX 1|2 Videos

  • BASIC MATHEMATICS USED IN PHYSICS &VECTORS

    ALLEN |Exercise BEGINNER S BOX 2|3 Videos

  • CENTRE OF MASS

    ALLEN |Exercise EXERCISE-V B|19 Videos

Similar Questions

Explore conceptually related problems

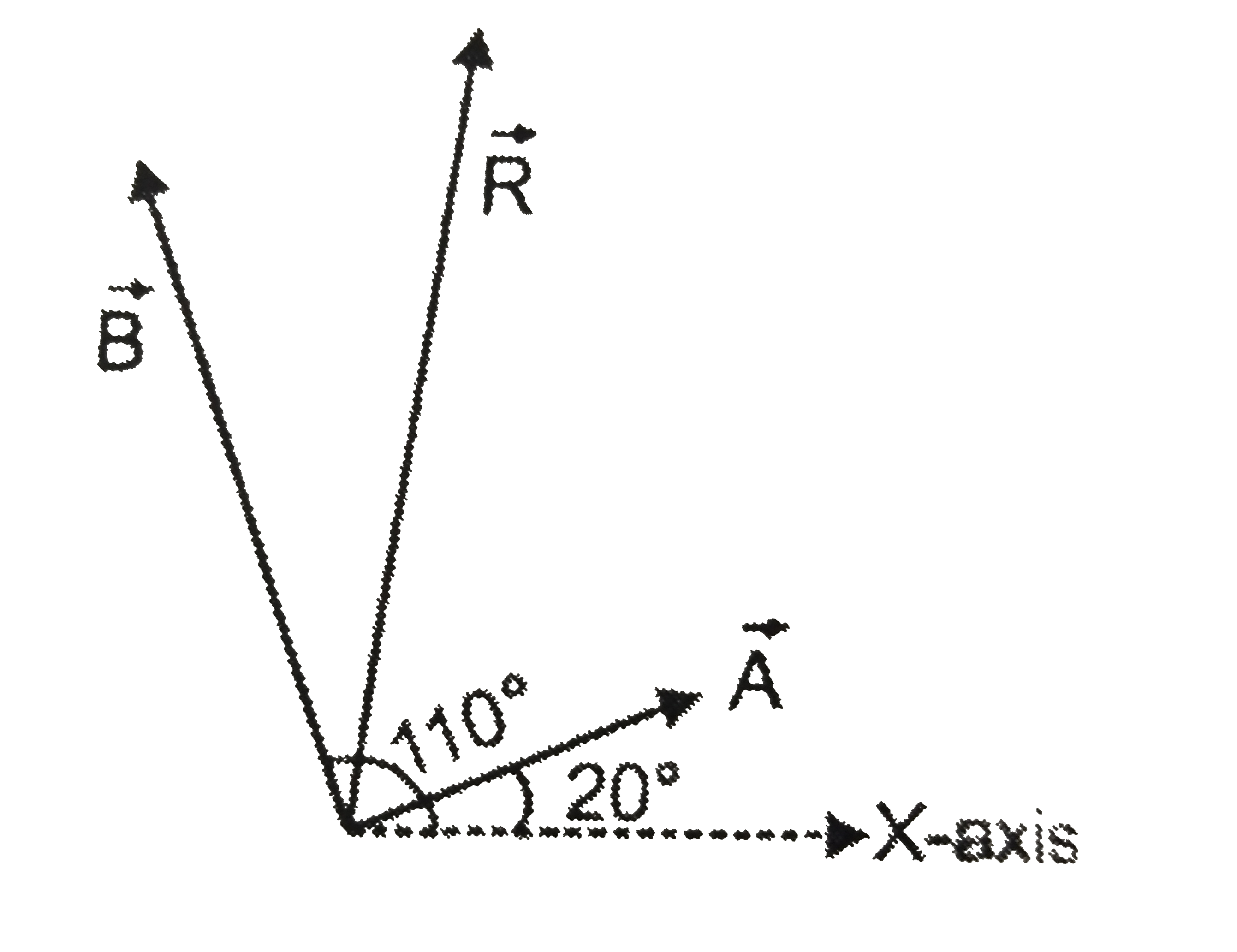
A vector vec(A) and vec(B) make angles of 20^(@) and 110^(@) respectively with the X-axis. The magnitudes of these vectors are 5m and 12m respectively. Find their resultant vector.

3hati and 5hatj are vector along x-axis and y-axis respectively. Find the resultant vector

Find out the angle made by (hati+hatj) vector from X and Y axes respectively.

The magnitude of the vector product of two vectors vecA and vecB may not be:

Find out the angle made by vecA=hati+hatj+hatk vector from X,Y and Z axes respectively.

A vector vec(A) of length 10 units makes an angle of 60^(@) with a vector vec(B) of length 6 units. Find the magnitude of the vector difference vec(A)-vec(B) & the angles with vector vec(A) .

Find out the angle made by vecA= hati+hatj+hatk vector from X, Y and Z axes respectively.

Find the angle between two vectors vecaandvecb with magnitudes 1 and 2 respectively and when veca*vecb=1 .

A displacement vector, at an angle of 30^(@) with y-axis has an x-component of 10 units. Then the magnitude of the vector is-

During the propagation of one progressive harmonic wave having amplitude 10 m, displacements and particles at 2 m and 16 m at respectively 2s and 8 s are 5 m and 5 sqrt3 m respectively. Find angular frequency and wave vector for this wave.