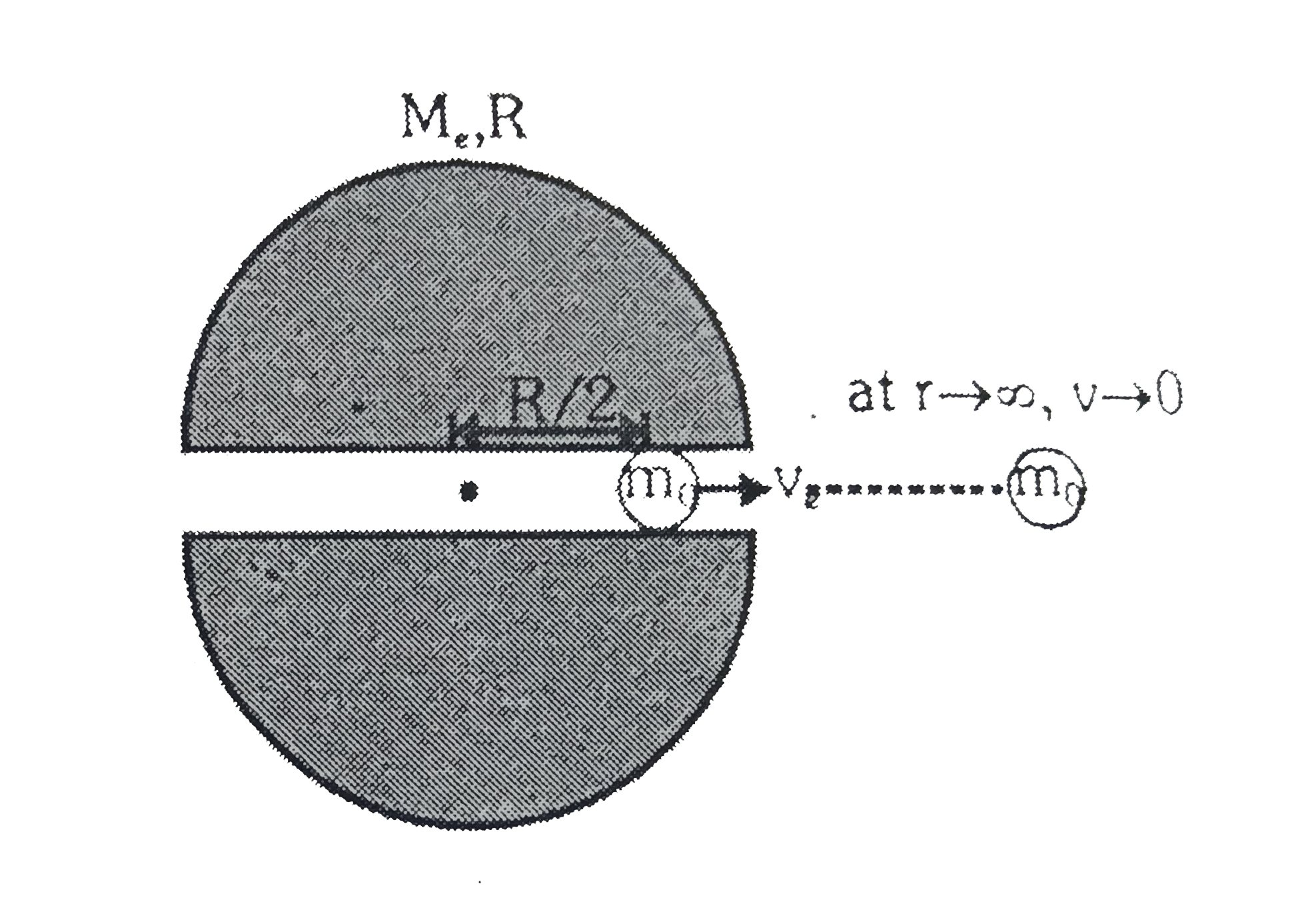Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -GRAVITATION-Illustration
- A solid sphere of uniform density and radius R applies a gravitational...
Text Solution
|
- The maximum vertical distance through which an astronaut can jump on t...
Text Solution
|
- Three solid sphere of mass M and radius R are placed in contact as sho...
Text Solution
|
- Four bodies each of mass m are placed at the different corners of a sq...
Text Solution
|
- A body of mass m is placed on the surface of earth. Find work required...
Text Solution
|
- if velocity given to an object from the surface of the earth is n time...
Text Solution
|
- a narrow tunnel is dug along the diameter of the earth, and a particle...
Text Solution
|
- The escape velocity for a planet is v(e), A particle starts from rest ...
Text Solution
|
- A particle is projected vertically upwards the surface of the earth (r...
Text Solution
|
- A mass of 6xx10^24 kg (equal to the mass of the earth) is to be compre...
Text Solution
|
- Gravitational potential difference between a point on surface of plane...
Text Solution
|
- A body of mass m kg starts falling from a distance 2R above the earth'...
Text Solution
|
- With what velocity must a body be thrown from earth's surface so that ...
Text Solution
|
- Two satellites S(1) and S(2) are revolving round a planet in coplanar ...
Text Solution
|
- A space-ship is launched into a circular orbit close to ther earth's s...
Text Solution
|
- A astronaut inside an earth satellite experiences weightlessness becau...
Text Solution
|
- if a satellite orbits as close to the earth's surface as possible.
Text Solution
|
- A planet is revolving around the sun in an elliptical orbit. Which out...
Text Solution
|
- An artificial satellite is moving in a circular orbit around the earth...
Text Solution
|
- Is it possible to place an artificial satellite in an orbit such that ...
Text Solution
|