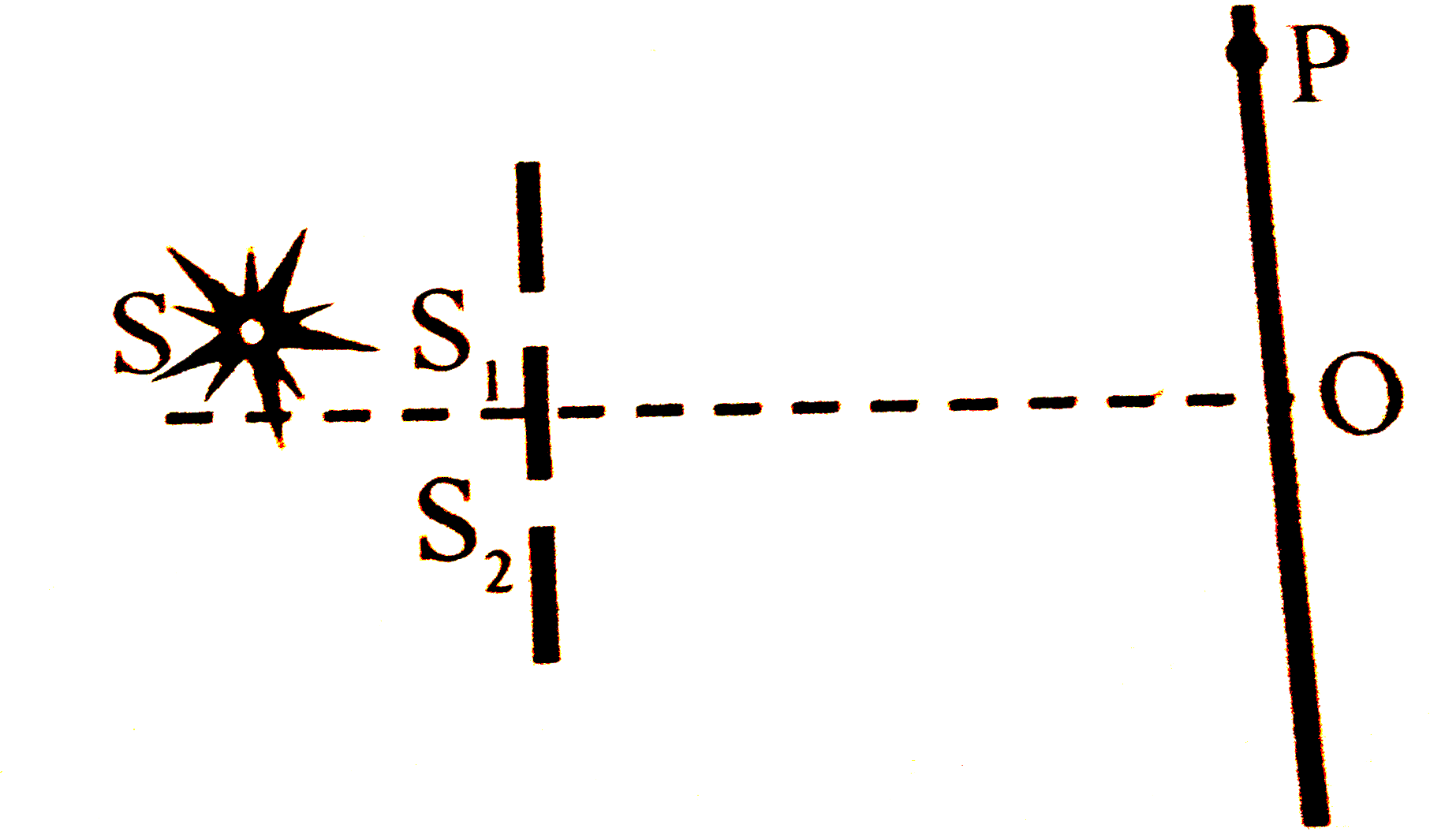Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -TEST PAPER 1-PHYSICS
- Why are electric field lines perpendicular at a point on an equipotent...
Text Solution
|
- When unpolarised light is incident on the interface separating the rar...
Text Solution
|
- For the same angle of incidence, the angles of refraction in three dif...
Text Solution
|
- Write the necessary conditions for the phenomenon of total internal re...
Text Solution
|
- Answer the following, giving reason:- (a) When light travels from ...
Text Solution
|
- An object is immersed in some liquid. Prove that .(a)n(l)=("Real d...
Text Solution
|
- Five point charges, each of value +q are placed on five vertices of a ...
Text Solution
|
- The figure shows a modified Young’s double slit experimental set-up. H...
Text Solution
|
- A small ink dot on a paper is viewed through a glass slab of thickness...
Text Solution
|
- if a particle performs SHM then its given by y=150sin(40t-12x). what ...
Text Solution
|
- If a particle performs SHM then it is given by y=150sin(40t-12x). wha...
Text Solution
|