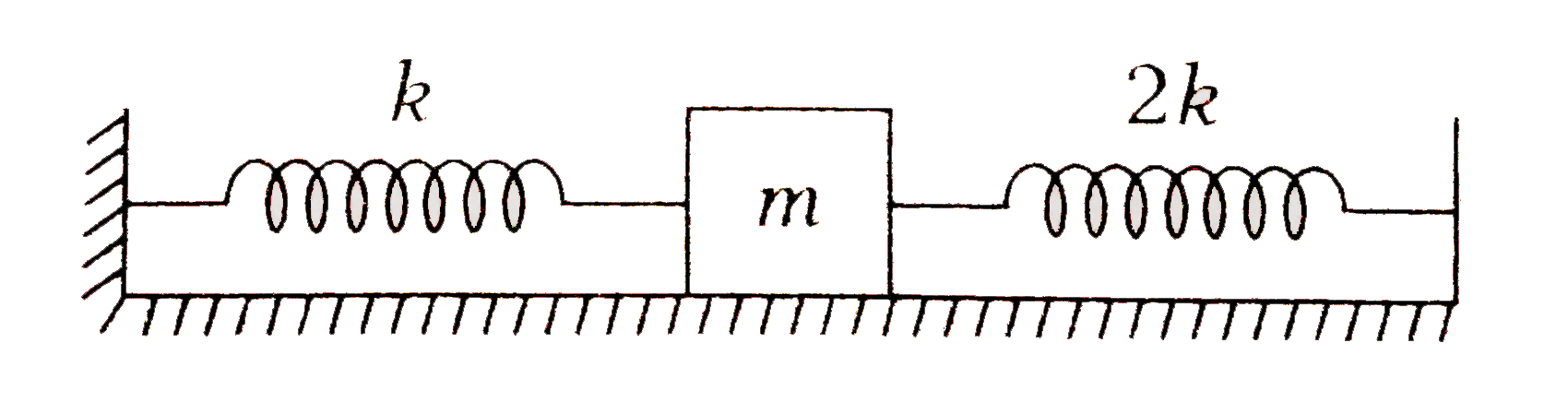A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Frequency of oscillation is proportional to
Text Solution
|
- Frequency of oscillation is proportional to
Text Solution
|
- In case of damped oscillation frequency of oscillation is
Text Solution
|
- Is the frequency of oscillation of kinetic energy or potential energy ...
Text Solution
|
- The frequency of oscillation in an oscillation
Text Solution
|
- In an oscillator, frequency of oscillations is given by
Text Solution
|
- The intermediate frequency is the oscillator frequency and radio freq...
Text Solution
|
- In the adjoining figure the frequency of oscillation for a mass m will...
Text Solution
|
- दोलन में अवमंदन बल अनुक्रमानुपाती होता है :
Text Solution
|