A lead shot of 1 mm diameter falls through a long colummn of glycerine. The variation of the velocity v with distance covered (s) is represented by
A lead shot of 1 mm diameter falls through a long colummn of glycerine. The variation of the velocity v with distance covered (s) is represented by
A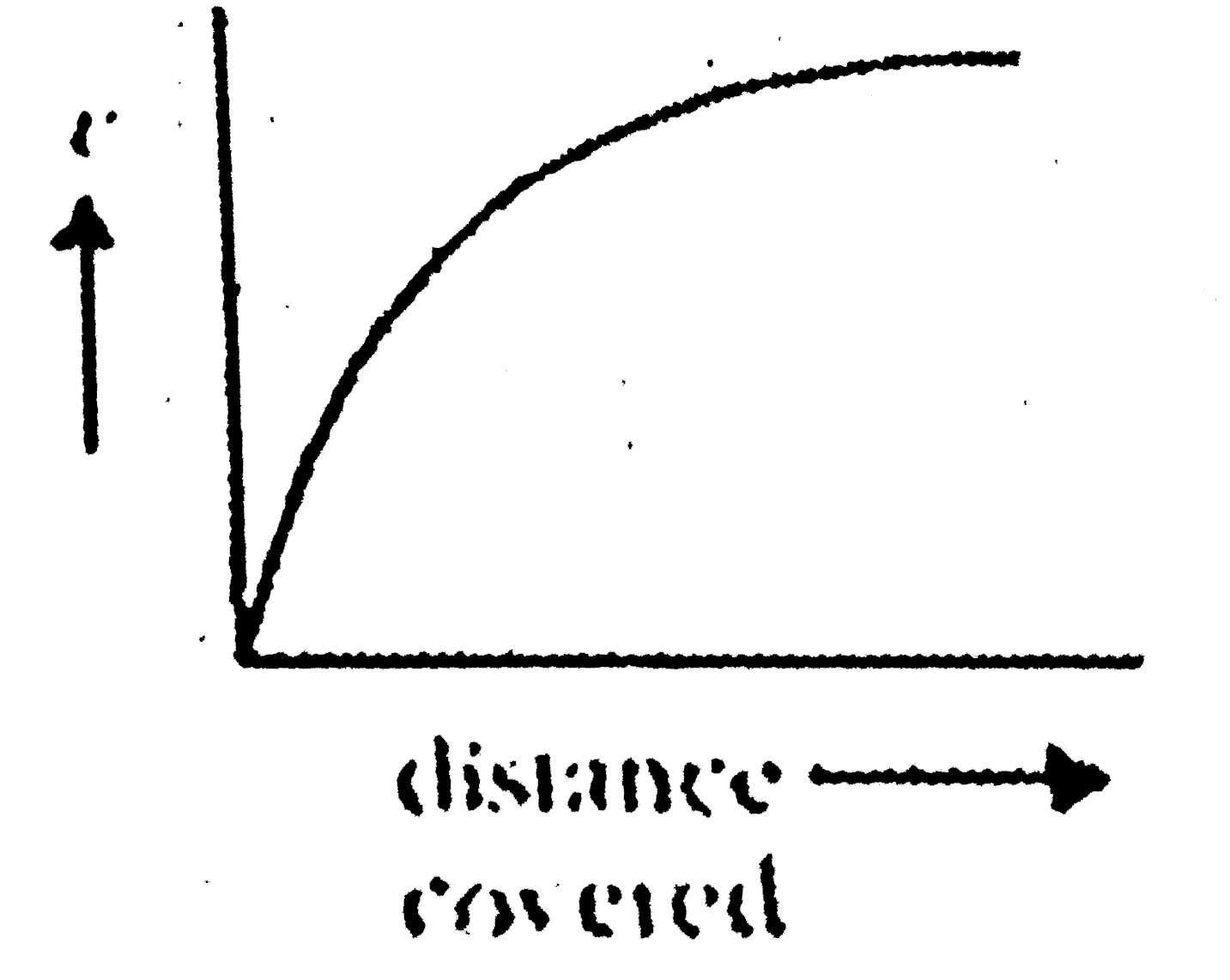

B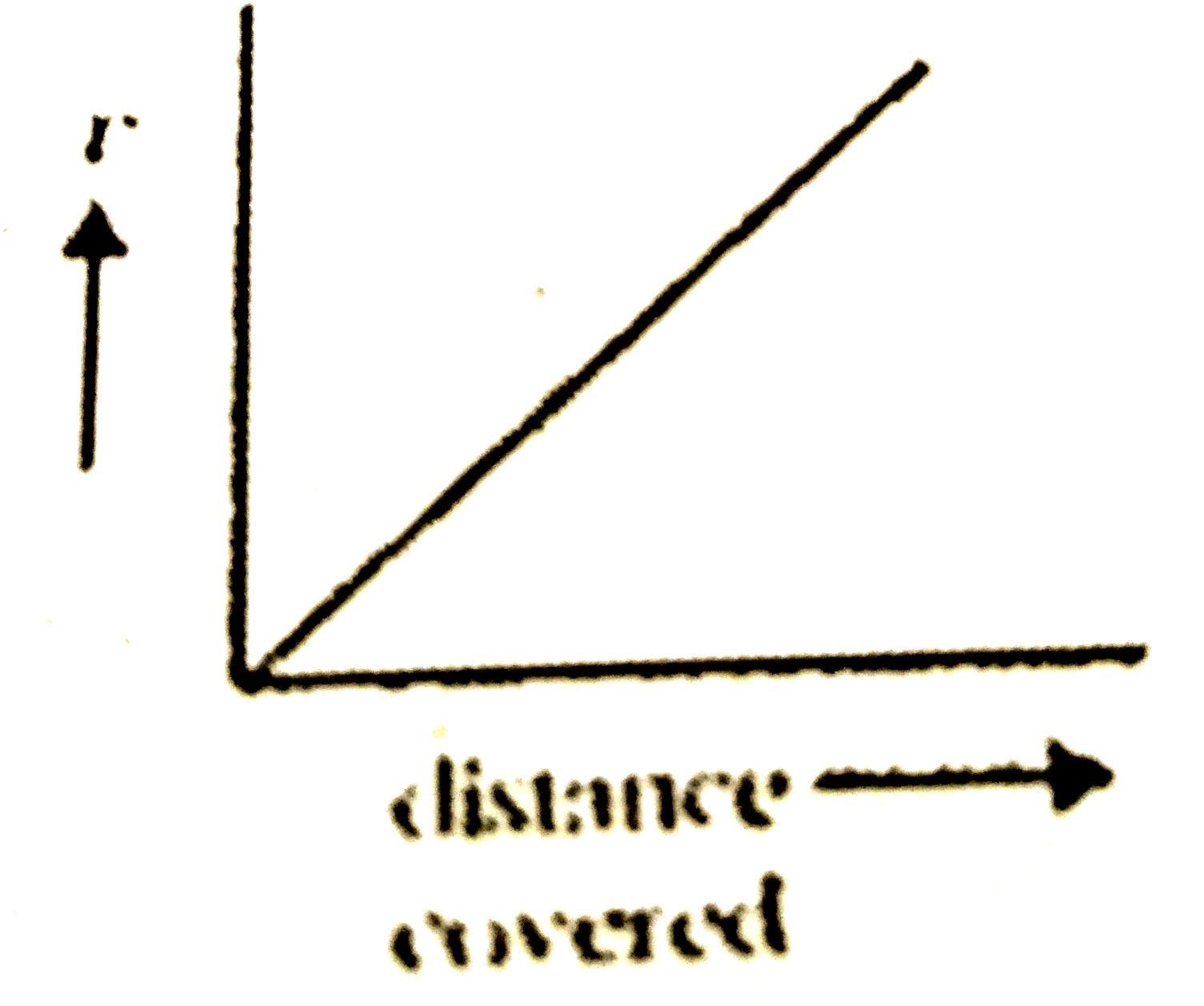

C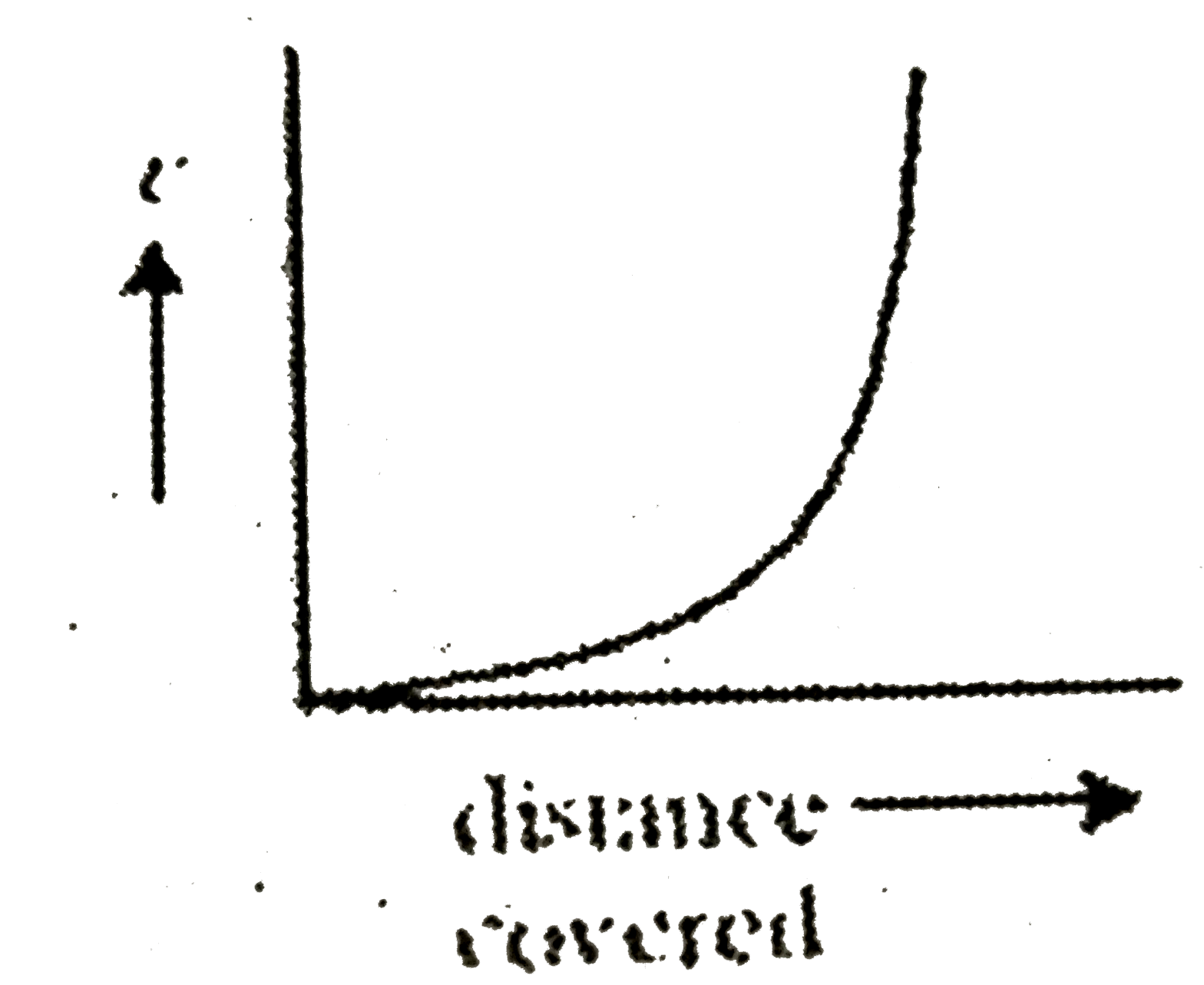

D

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem of a lead shot falling through a long column of glycerine, we need to analyze the forces acting on the shot and how they affect its motion. Here’s a step-by-step solution:
### Step 1: Understand the Forces Acting on the Lead Shot
When the lead shot is released, two main forces act on it:
- **Gravitational Force (Weight)**: This force pulls the shot downward and is given by \( F_{\text{gravity}} = mg \), where \( m \) is the mass of the lead shot and \( g \) is the acceleration due to gravity.
- **Viscous Drag Force**: As the shot moves through glycerine, it experiences a drag force due to the viscosity of the fluid. This force opposes the motion and is given by Stokes' law for small particles, \( F_{\text{viscous}} = 6\pi r \eta v \), where \( r \) is the radius of the shot, \( \eta \) is the viscosity of glycerine, and \( v \) is the velocity of the shot.
### Step 2: Analyze the Motion
Initially, when the shot is released, it accelerates due to the gravitational force. As its velocity increases, the viscous drag force also increases. Eventually, the drag force will balance the gravitational force, leading to a terminal velocity where the net force on the shot becomes zero.
### Step 3: Determine the Velocity vs. Distance Relationship
- **Initial Phase**: When the shot is released, it accelerates, and its velocity increases with distance. This phase can be represented by a curve that rises steeply.
- **Terminal Velocity Phase**: Once the drag force equals the gravitational force, the shot reaches a terminal velocity. At this point, the velocity remains constant as the shot continues to fall.
### Step 4: Graphical Representation
The graph of velocity \( v \) versus distance \( s \) will show:
- An initial increasing slope (representing acceleration).
- A plateau where the velocity becomes constant (representing terminal velocity).
### Conclusion
The correct representation of the velocity \( v \) as a function of distance \( s \) is a curve that starts steep and then levels off, indicating that the lead shot accelerates initially and then moves at a constant speed.
### Final Answer
The variation of the velocity \( v \) with distance covered \( s \) is represented by a graph that starts with a steep incline and then levels off, corresponding to the first option given in the problem.
---
To solve the problem of a lead shot falling through a long column of glycerine, we need to analyze the forces acting on the shot and how they affect its motion. Here’s a step-by-step solution:
### Step 1: Understand the Forces Acting on the Lead Shot
When the lead shot is released, two main forces act on it:
- **Gravitational Force (Weight)**: This force pulls the shot downward and is given by \( F_{\text{gravity}} = mg \), where \( m \) is the mass of the lead shot and \( g \) is the acceleration due to gravity.
- **Viscous Drag Force**: As the shot moves through glycerine, it experiences a drag force due to the viscosity of the fluid. This force opposes the motion and is given by Stokes' law for small particles, \( F_{\text{viscous}} = 6\pi r \eta v \), where \( r \) is the radius of the shot, \( \eta \) is the viscosity of glycerine, and \( v \) is the velocity of the shot.
### Step 2: Analyze the Motion
...
Similar Questions
Explore conceptually related problems
A body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:
A bar magnet is made to fall through a long vertica! copper tube. The speed (V) of the magnet as a function of time (t) is best represented by
Two identical source moving parallel to each other at seperation 'd' are producing sounds of frequency 'f' and are moving with constant velocity v_(0) . A stationary .observer 'O' is on the line of motion of one of the sources. Then the variation of beat frequency heard by O with time is best represented by: (as they come from large distance and go to a large distance)
A spherical steel ball released at the top of along column of glycerin of length l falls through a distance l//2 with accelerated motion and the remaining distance l//2 with uniform velocity let t_(1) and t_(2) denote the times taken to cover the first and second half and w_(1) and w_(2) are the work done against gravity in the two halves, then compare times and work done.
A point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_0 . Find: (a) the velocity of the point as a function of time and as a function of the distance covered s_1 , (b) the total acceleration of the point as a function of velocity and the distance covered.
Two ends of a rod of non uniform area of cross section are maintained at temperature T_(1) and T_(2) (T_(1)>T_(2)) as shown in the figure If l is heat current through the cross-section of conductor at distance x from its left face, then the variation of l with x is best represented by
Refering to v-s diagram, find: . a. Acceleration of the particle when its velocity becomes half of the initial velocity. b. Total distance covered by the particle.
From amongst the following curves, which one shows the variation of the velocity v with time t for a small sized spherical body falling vertically in a long column of a viscous liquid
A point object moves along an arc of a circle of radius 'R'. Its velocity depends upon the distance covered 'S' as V = Ksqrt(S) where 'K' is a constant. If ' theta' is the angle between the total acceleration and tangential acceleration, then
A metal sphere of radius 1 mm and mass 50 mg falls vertically in glycerine. Find (a) the viscous force exerted by the glycerine on the sphere when the speed of the sphere is 1 cm s-1, (b) the hydrostatic force exerted by the glycerine on the sphere and (c) the terminal velocity with which the sphere will move down without acceleration. Density of glycerine =1260kgm^-3 and its coefficient of viscosity at room temperature = 8.0 poise.
Recommended Questions
- A lead shot of 1 mm diameter falls through a long colummn of glycerine...
Text Solution
|
- A lead shot of a 1mm diameter falls through a long column of glycerine...
Text Solution
|
- A lead shot of 1 mm diameter falls through a long colummn of glycerine...
Text Solution
|
- A steel ball-bearing of diameter 3 mm falls through glycerine and cove...
Text Solution
|
- find the terminal velocity of a steel ball 2mm in diameter falling thr...
Text Solution
|
- A lead shot of 1 mm diameter falls through a long column of glycerin. ...
Text Solution
|
- A lead shot of 1 mm diameter falls through a long colummn of glycerine...
Text Solution
|
- A lead ball is allowed to fall through an elongated column filled with...
Text Solution
|
- A spherical ball of steel of radius 2 mm is falling down through glyce...
Text Solution
|