Home
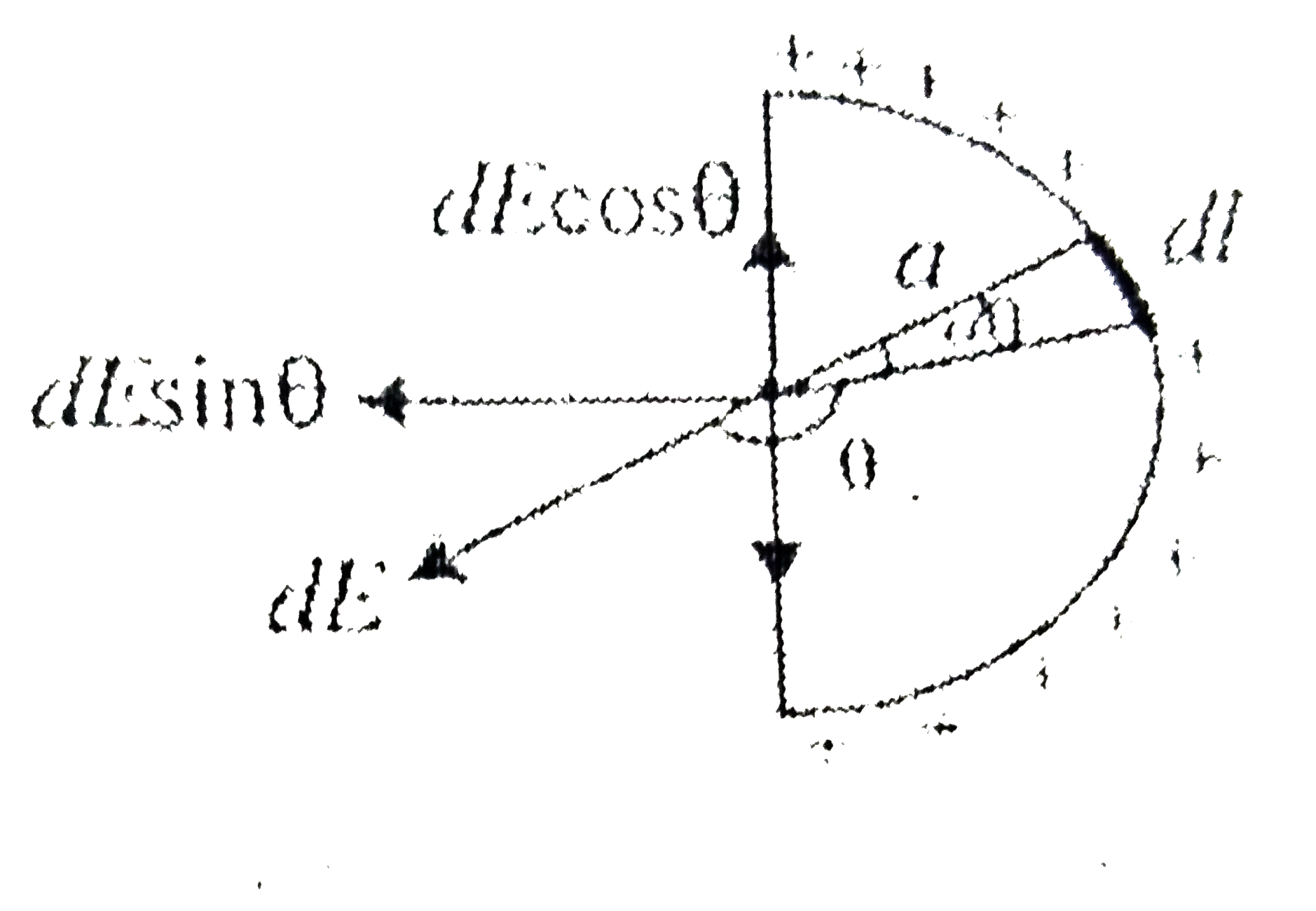
Class 12
PHYSICS
Electric field at centre of a uniforly c...

Electric field at centre of a uniforly charged semicirlce of radius a is

A

` lambda / (2 pi epsilon_0a^3)`

B

`lambda/(2pi epsilon_0a^2)`

C

`(lambda_2)/(2pi epsilon_0a)`

D

`(lambda)/(2pi epsilon_0a)`

Text Solution

Verified by Experts

The correct Answer is:
D

Electtric field intensity at O due to small elemental length dl of charged ring .
`dE = (1)/(4 pi epsi_(0)) * (lambda dl)/(a^(2)) = (1)/(4 pi epsi_(0)) * (lambda ad theta)/(a^(2))`
`dE = (1)/(4 pi epsi_(0)) * (lambda)/(a)"" d theta`
`therefore ` Net electric field at centre O is
E = `int d E sin theta = overset(pi)underset(0)(int) (1)/(4 pi epsi_(0)) (lambda)/(a)"" sin theta d theta`
`= (lambda)/(4 pi epsi_(0) a) [ - cos theta]_(0)^(pi)`
`therefore E = (lambda)/(2 pi epsi_(0) a)`.
Promotional Banner

Similar Questions

Explore conceptually related problems

Find the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is lamda

If the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (rgtR) .

The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by

Electric field at the centre of uniformly charge hemispherical shell of surface charge density sigma is (sigma)/(n epsi_(0)) then find the value of n .

At which distance along the centre axis of a uniformaly charged plastic disc of radius R is the magnitude of the electric field equal to one-half the magnitude of the field at the centre of the surface of the disc ?

Electric field at centre O of semicircule of radius 'a' having linear charge density lambda given is given by

At a point 20 cm from the centre of a uniformly charged dielectric sphere of radius 10 cm , the electric field is 100 V//m . The electric field at 3 cm from the centre of the sphere will be

Which graph best represents the variation of electric potential as a function of distance from the centre of a uniformly charged solid sphere of charge of radius R ?

The electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance ( R )/(2) from the centre will be

Assertion: Electric potential on the surface of a charged sphere of radius R is V. Then electric field at distance r=R/2 from centre is V/(2R) . Charge is distributed uniformly over the volume. Reason: From centre to surface, electric field varies linearly with r. Here r is distance from centre.