A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
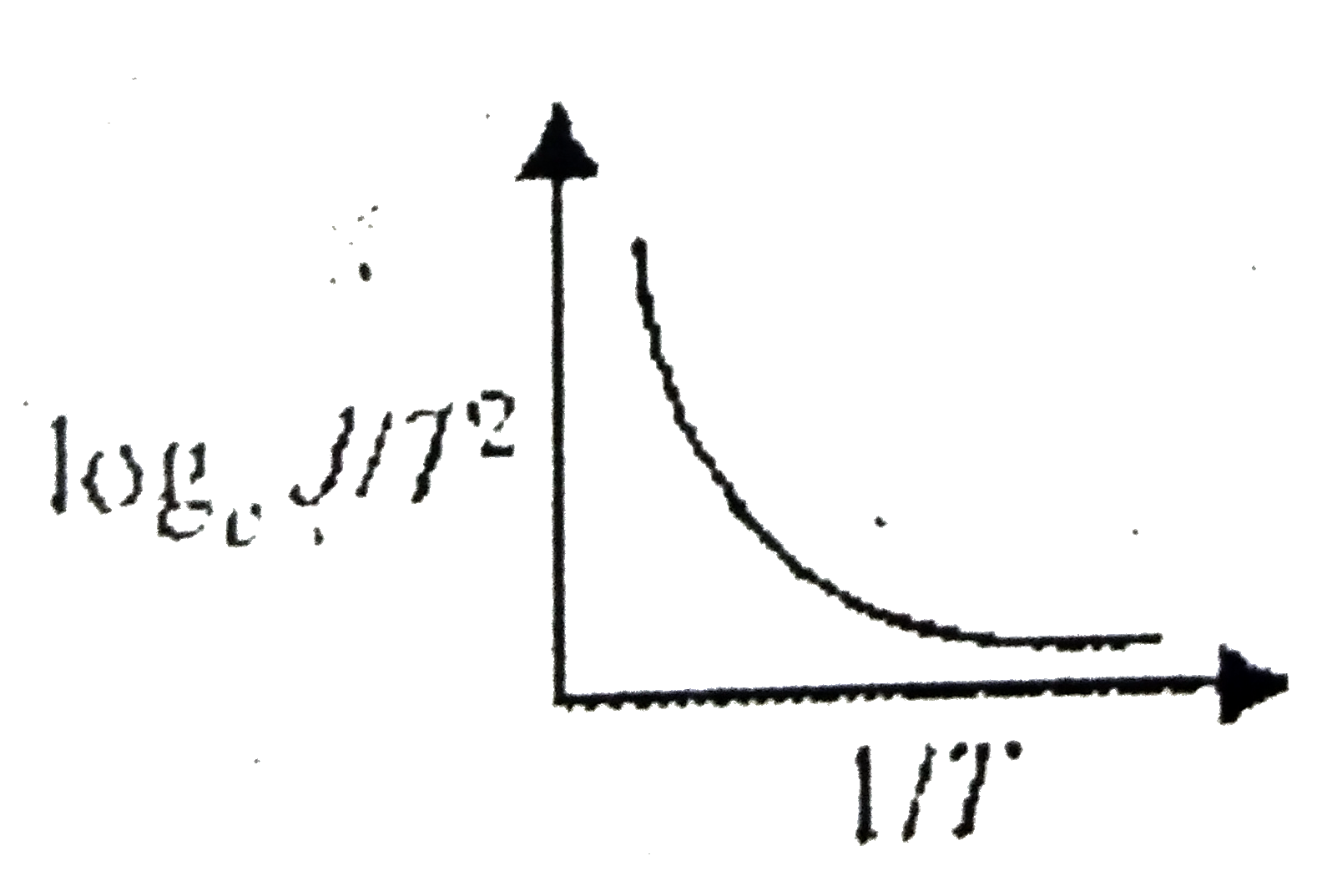
- The current curve between loge""(j)/(T^2)" and "l/T
Text Solution
|
- On solving the equation log((1)/(2))[log(t)(log(4)32)]=2 then t=
Text Solution
|
- If the thermionic current density is J and emitter temperature is T th...
Text Solution
|
- Show that the curve whose parametric coordinates are x=t^(2)+t+l,y=t^(...
Text Solution
|
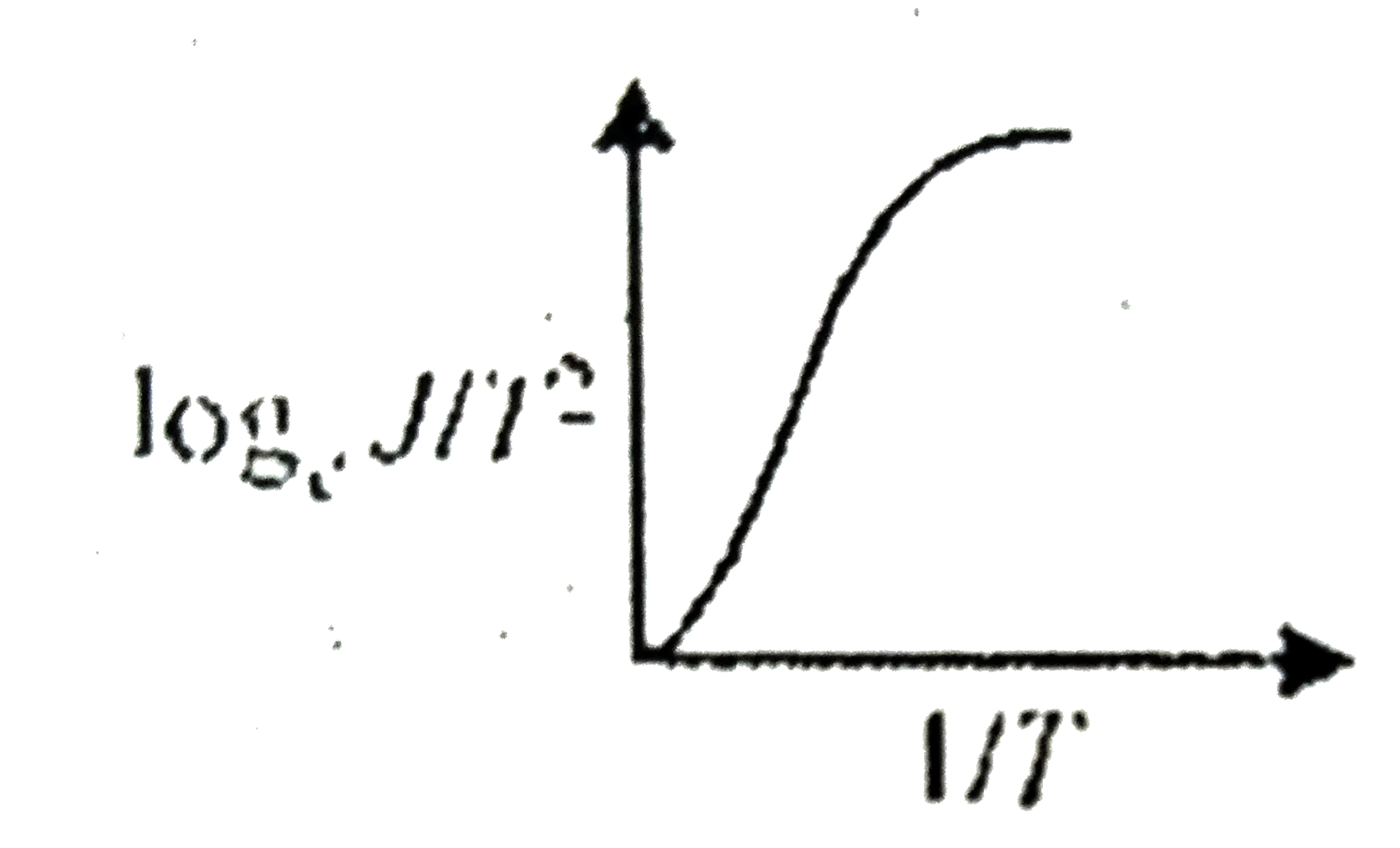
- The current curve between loge""(j)/(T^2)" and "l/T
Text Solution
|
- The curve between log(e) L and log(e) P is (L is the angular momentum ...
Text Solution
|
- log(e)L तथा log(e)P के बीच वक्र है (L कोणीय संवेग तथा P रेखीय संवेग ह...
Text Solution
|
- The graph between L and T^(2) is
Text Solution
|
- Show that the curve whose parametric coordinates are x=t^(2)+t+l,y=t^(...
Text Solution
|