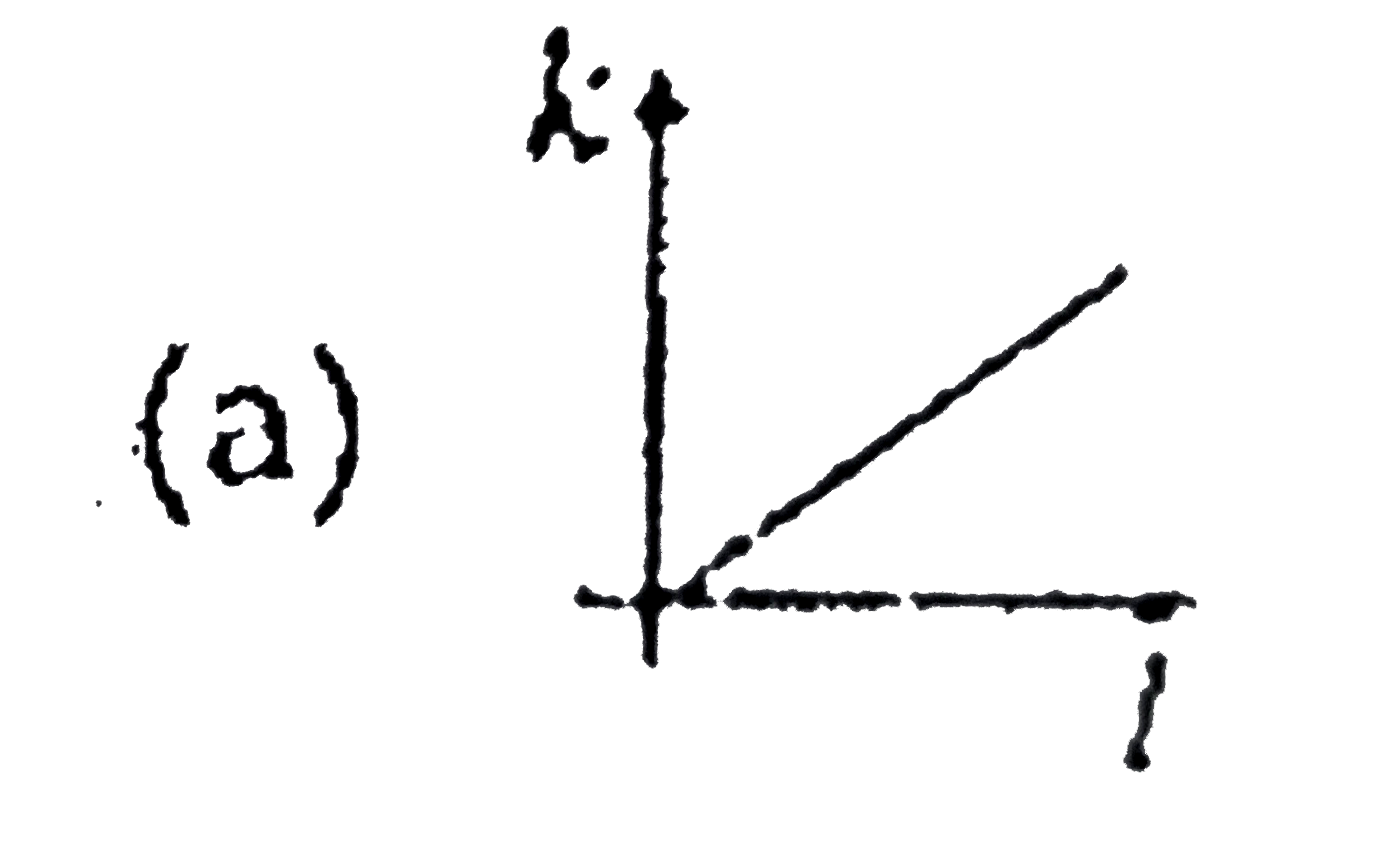
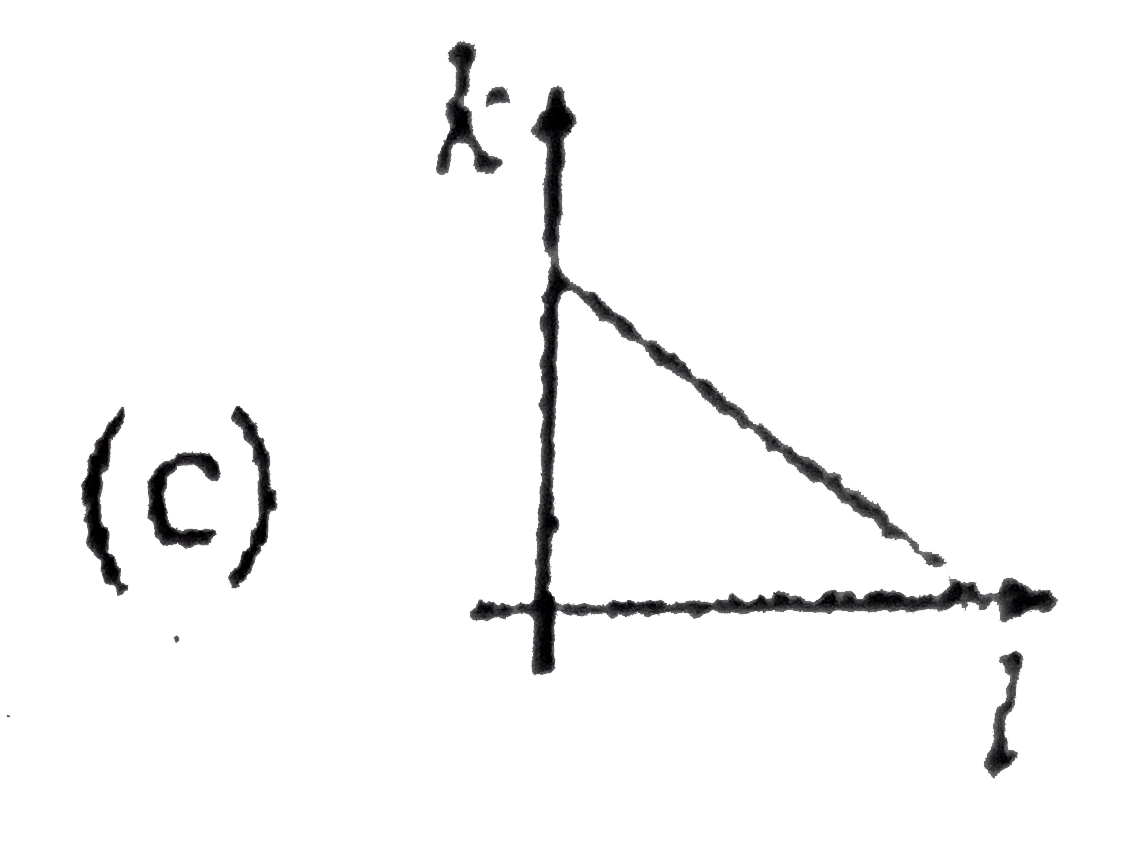
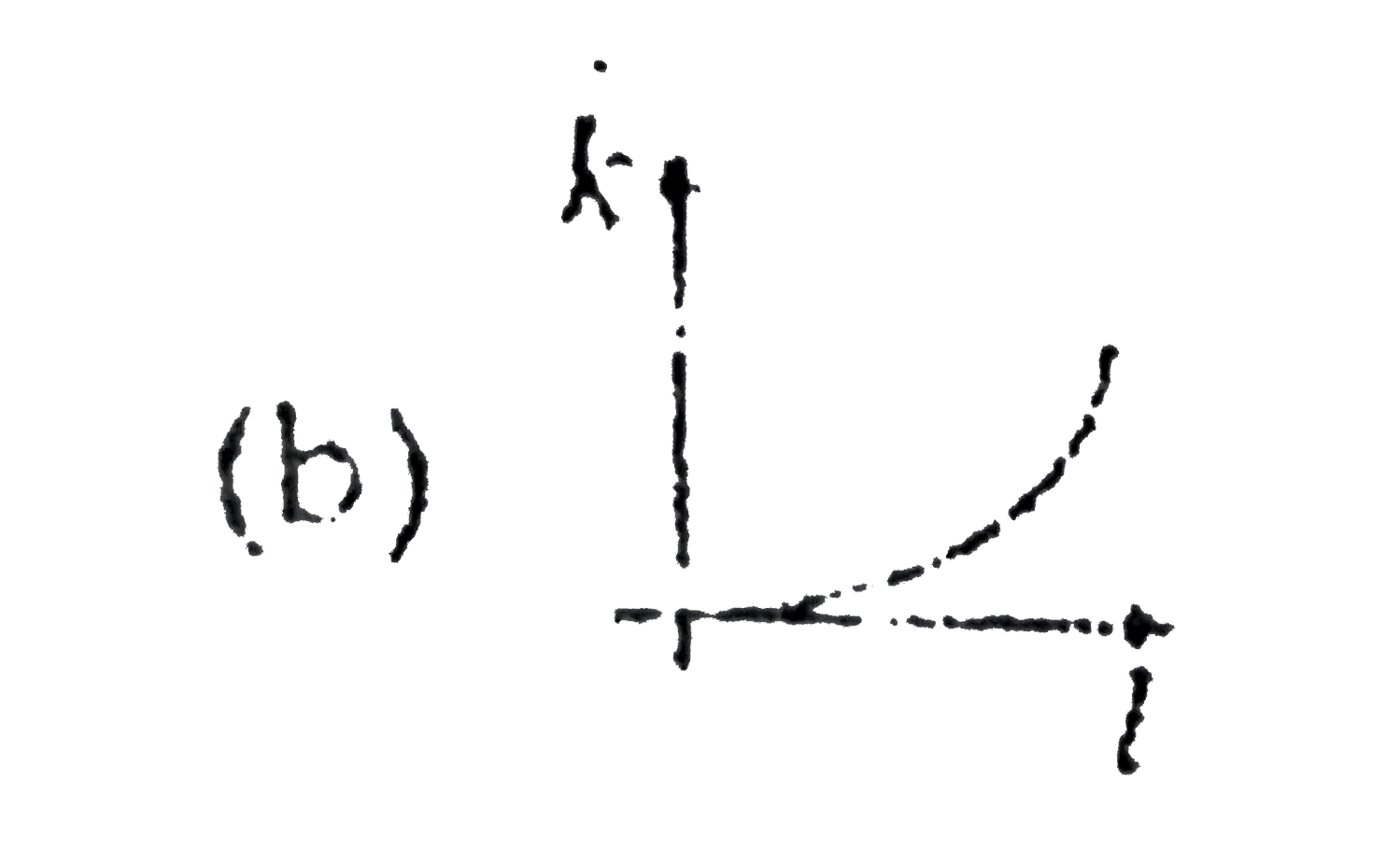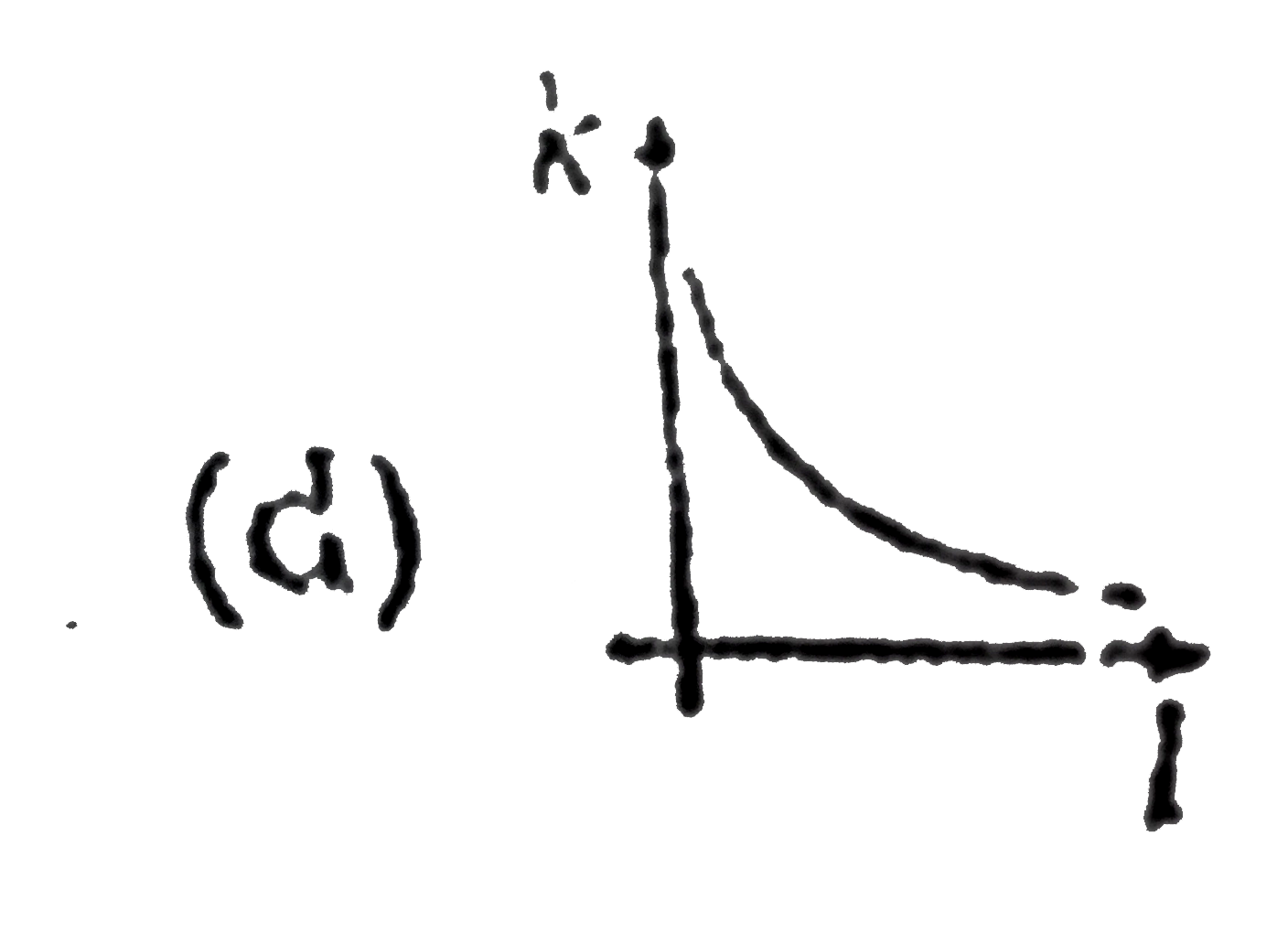A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Which of the following graph depicts spring constant k versus length l...
Text Solution
|
- A spring fo spring constant k is broken in the length ratio 1:3. The s...
Text Solution
|
- Which of the following graph depicts spring constant k versus length l...
Text Solution
|
- A metal wire of length L, area of cross-section A and Young's modulus ...
Text Solution
|
- A spring of constant K is cut into two parts of length in the ra...
Text Solution
|
- The pointer reading versus load graph for a spring balance is as shown...
Text Solution
|
- A massless spring of length l and spring constant k is placed vertical...
Text Solution
|
- A length of L, a cross section of A and a coefficient of Y Young behav...
Text Solution
|
- What will be the spring constant k of a. spring if length of the sprin...
Text Solution
|