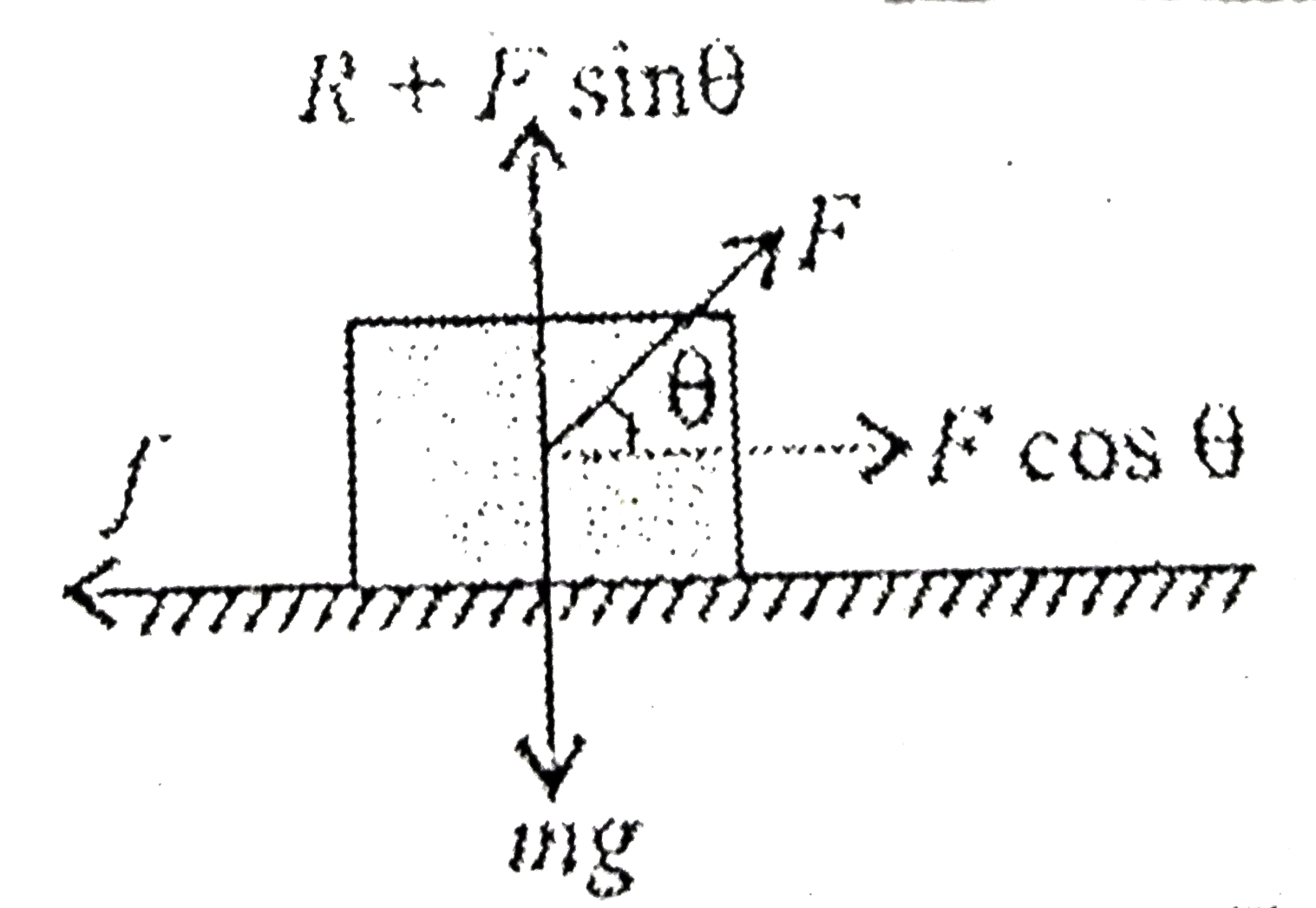
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of mass M is pulled along a horizontal surface by applying a f...
Text Solution
|
- A block of mass M is pulled along a horizontal surface by applying a f...
Text Solution
|
- A block of mass 5 kg is pulled along a horizontal. The friction coeffi...
Text Solution
|
- A block of mass m is lying on horizontal surface of coefficient of fri...
Text Solution
|
- What is the value of applied force ‘F’ which is exerted at an angle th...
Text Solution
|
- A block of mass m is pulled along a horizontal suface by applying a fo...
Text Solution
|
- A block of mass M is pulled along a horizontal surface by applying a f...
Text Solution
|
- A block of mass m is pulled along a horizontal surface by applying a f...
Text Solution
|
- A block of mass m is pulled along a horizontal surface by applying a f...
Text Solution
|