Home
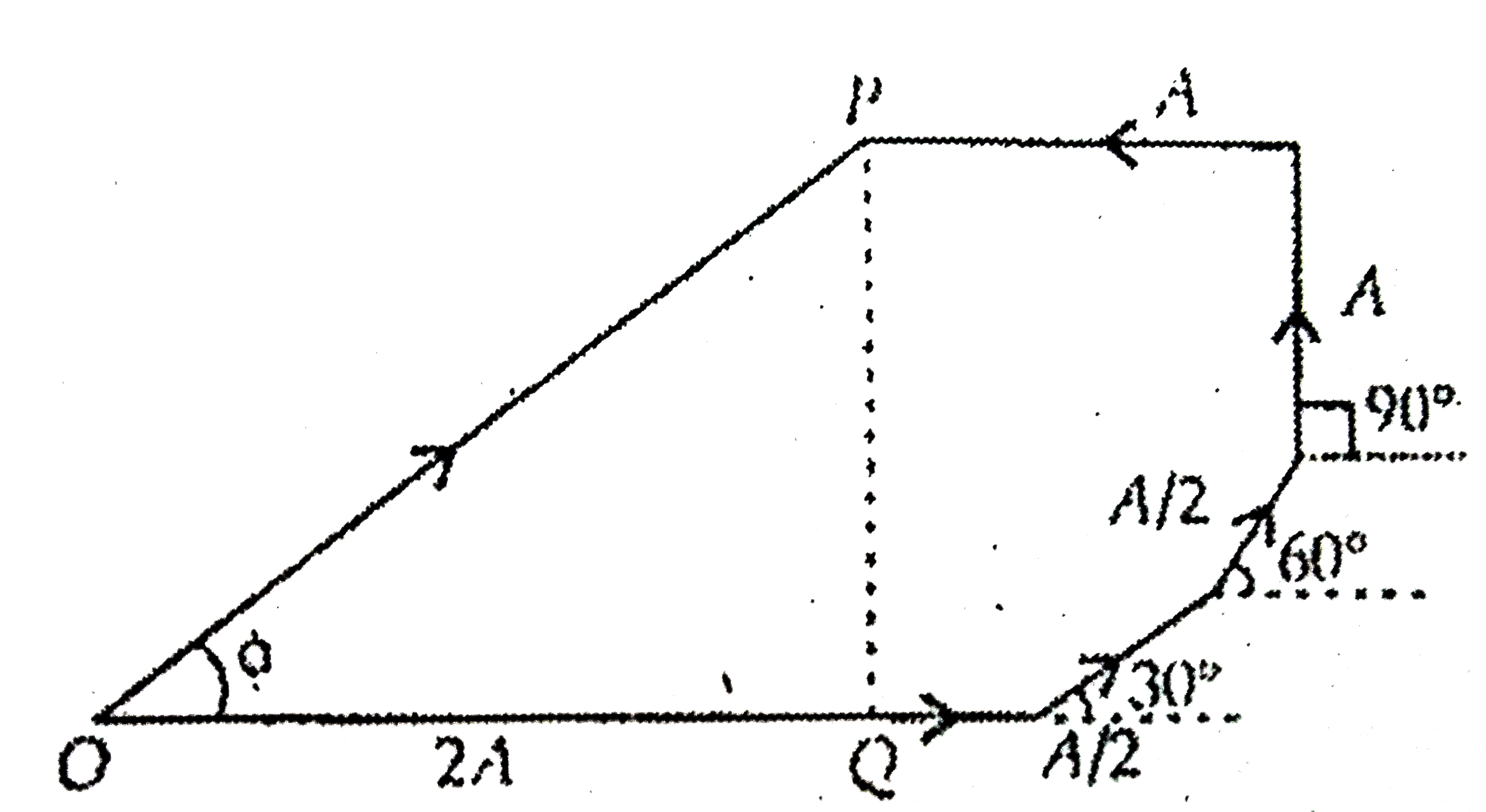
Class 12
PHYSICS
Five sinusoidal waves have the same freq...

Five sinusoidal waves have the same frequency 500 Hz but their amplitudes are in the ratio `2 : (1)/(2) : (1)/(2) : 1 : 1` and their phase angles `0, (pi)/(6), (pi)/(3), (pi)/(2)` and `pi` respectively. The phase angle of resultant wave obtained by the supersposition of these five waves is

A

` 30^@ `

B

` 45^@ `

C

` 60 ^@ `

D

`90^@ `

Text Solution

Verified by Experts

The correct Answer is:
B

`y_(t)=2Asin omegat, y_(2)=A/2sin(omega+pi/2)`
`y_(3)=(A)/(2)sin(omegat=(pi)/(3)),y_4=A sin (omegat+(pi)/(2))`
`y_(s)=A sin (omegat+pi)`
By phasor diagram. `tan phi=(PQ)/(OQ)=1`
`Rightarrow phi=45^(@)`
Promotional Banner

Similar Questions

Explore conceptually related problems

Three sinusoidal waves having same frequency have amplitudes in the ratio 6:3:2 and their phases are 0, pi/2 ,pi . If 6a be the amplitude of the first wave , then which of the following is not correct

Three sinusodal waves having amplitudes a, a/2 and a/3 are superposed. They have the same period and thelr phase are 0, pi//2 and respectively. Find (i) The resultant amplitude and phase (ii) Draw a sketch to show the resultant wave.

Three simple harmonic waves , identical in frequency n and amplitude A moving in the same direction are superimposed in air in such a way , that the first , second and the third wave have the phase angles phi , phi + ( pi//2) and (phi + pi) , respectively at a given point P in the superposition Then as the waves progress , the superposition will result in

Three simple harmonic waves , identical in frequency n and amplitude A moving in the same direction are superimposed in air in such a way , that the first , second and the third wave have the phase angles phi , phi + ( pi//2) and (phi + pi) , respectively at a given point P in the superposition Then as the waves progress , the superposition will result in

In the sides of a triangle are in the ratio 1:sqrt(3):2, then the measure of its greatest angle is (a) pi/6 (b) pi/3 (c) pi/2 (d) (2pi)/3

Three component sinusoidal waves progressing in the same directions along the same path have the same period byt their amplitudes are A, A/2 and A/3. The phases of the variation at any position x on their path at time t = 0 are 0, -pi/2 and -pi respectively. Find the amplitude and phase of the resultant wave.

Four harmonic waves of equal freuencies and equal intensity I_(0) have phase angles 0, (pi)/(3), (2pi)/(3) and pi . When they are superposed, the intensity of the resulting wave is nI_(0) . The value of n is

Two sinusoidal waves of the same frequency travel in the same direction along a string. If A_(1) =m 3.0 cm, A_(2) = 4.0 cm, phi_(1) = 0 , and phi_(2) = pi//2 rad , what is the amplitude of the resultant wave ?

If the phase difference between the two wave is 2 pi during superposition, then the resultant amplitude is

If the phase difference between the two wave is 2 pi during superposition, then the resultant amplitude is