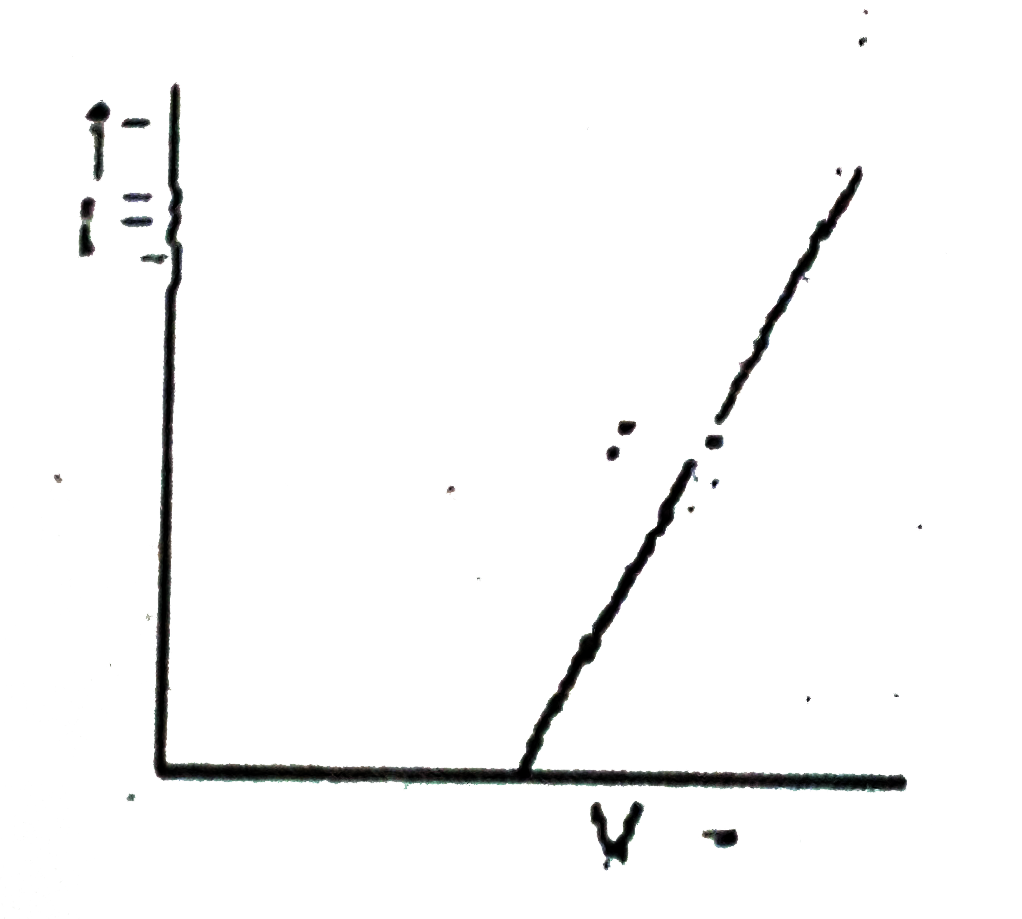
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The correct graph respectivley the relation between energy (E ) of pho...
Text Solution
|
- If the work function of a metal is 'phi' and the frequency of the inci...
Text Solution
|
- The correct graph respectivley the relation between energy (E ) of pho...
Text Solution
|
- Given in fig. is the graph between frequency v of the incident light a...
Text Solution
|
- Choose the correct option for the graph between the frequency of incid...
Text Solution
|
- Kinetic energy of surface photoelectrons is x when frequency of incide...
Text Solution
|
- The graph between the energy of photoelectrons E and the wavelength of...
Text Solution
|
- The photoelectric threshold frequency of a metal is v. When light of f...
Text Solution
|
- If the work function of a metal is 'phi' and the frequency of the inci...
Text Solution
|