A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
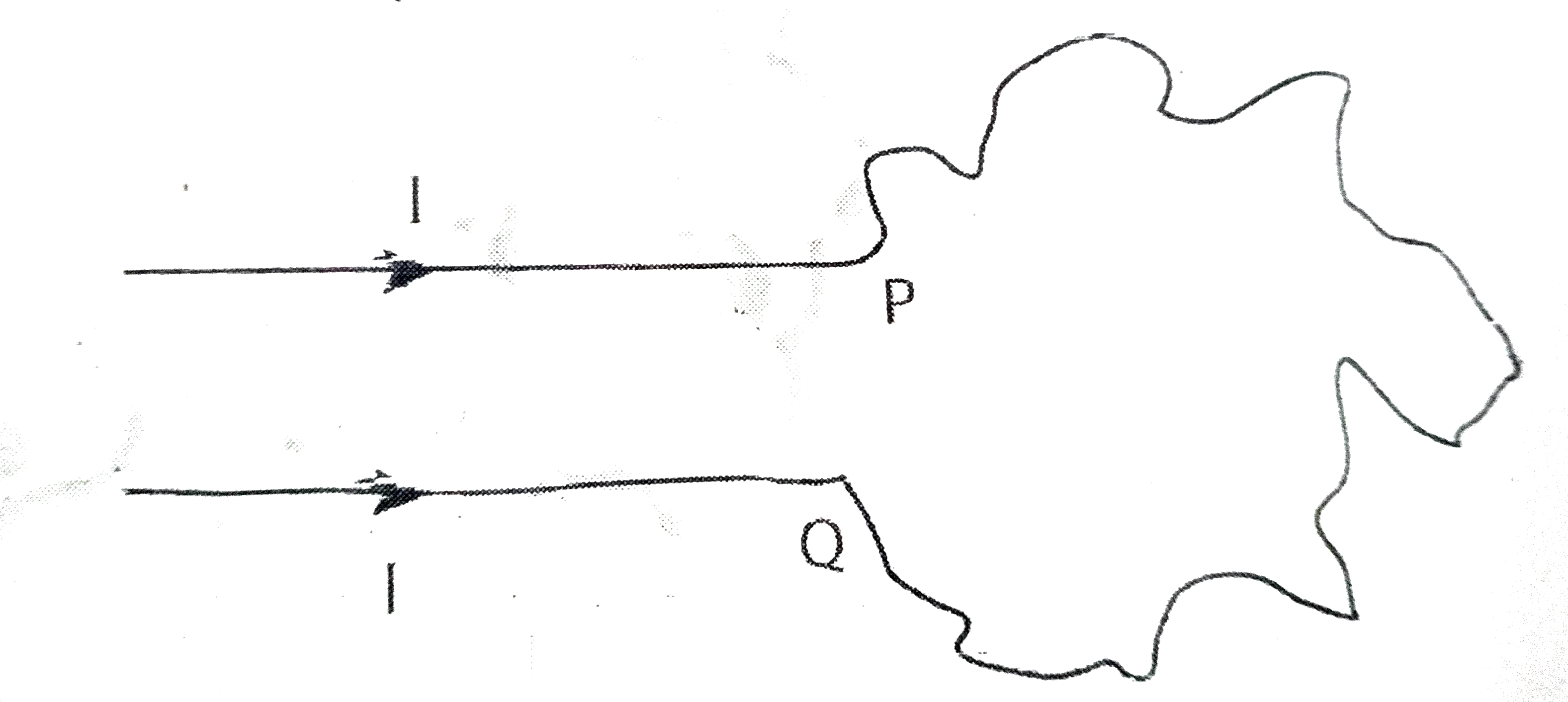
- Assertion (A) A wire bent into an irregular shape with the point P and...
Text Solution
|
- A loop of irregular shape carrying current is located in an external m...
Text Solution
|
- An irregular loop of conducting wire is lying on a frictionless table ...
Text Solution
|
- A long wire is bent as shown in Fig. what will be the magnitude and di...
Text Solution
|
- Assertion A flexeble wire loop of irregular shape carrying current whe...
Text Solution
|
- Assertion: Electric field inside a current carrying wire is zero. Reas...
Text Solution
|
- What is the effect on the magnetic needle in Oersted's experiment, whe...
Text Solution
|
- Assertion (A) A wire bent into an irregular shape with the point P and...
Text Solution
|
- A current carrying loop of irregular shape is located in an external m...
Text Solution
|