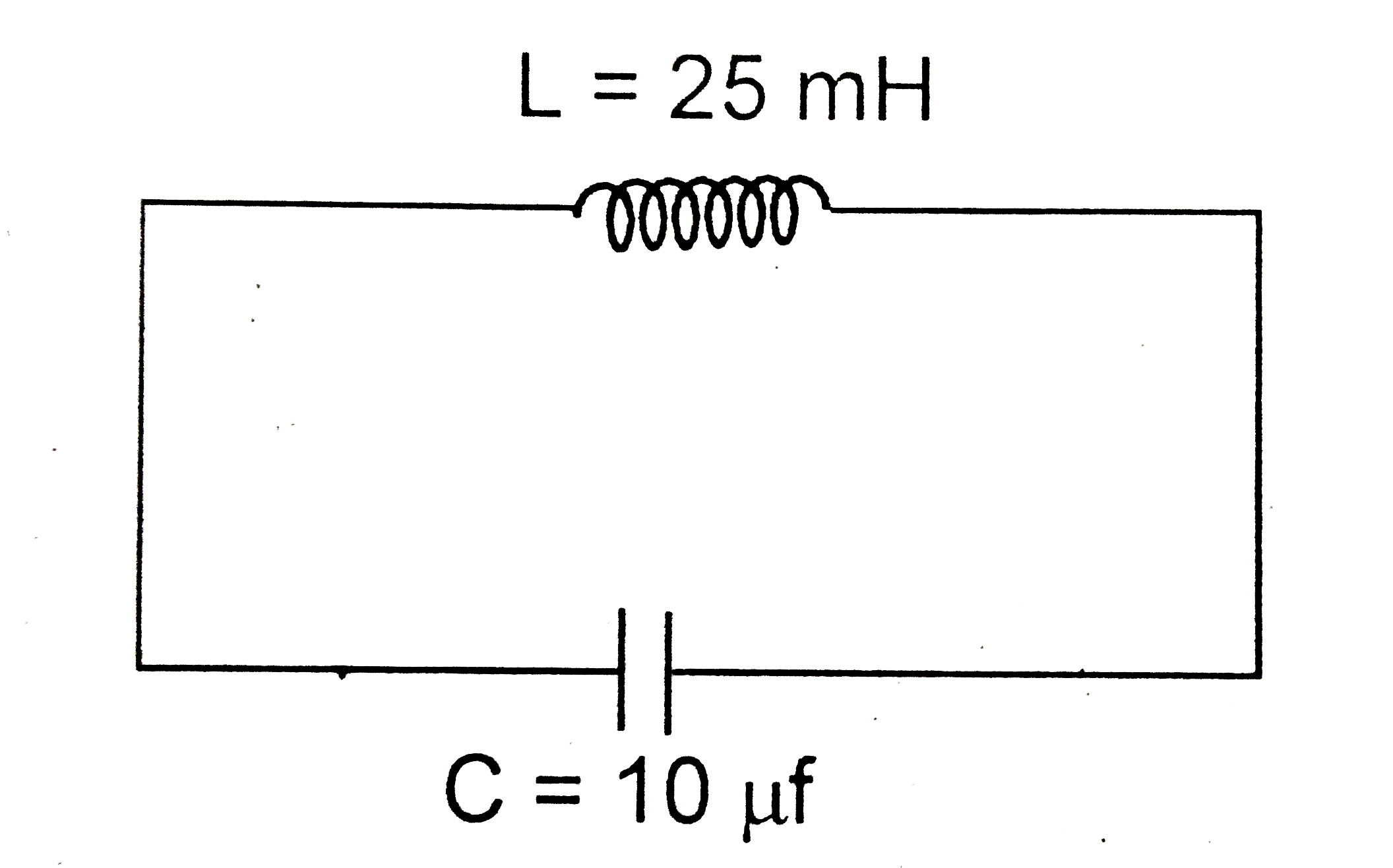A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If maximum energy is stored in capacitor at t = 0 then find the time a...
Text Solution
|
- In the circuit shown in fig. find the maximum energy stored on the cap...
Text Solution
|
- In a series circuit C=2muF,L=1mH and R=10 Omega, when the current in t...
Text Solution
|
- A 1.5 mH inductor in an LC circuit stores a maximum energy of 30 mu J ...
Text Solution
|
- At t=0 switch S is closed . Find (a) charge on capacitor after one t...
Text Solution
|
- At t=0 switch S is closed . (a) After how much time , charge on cap...
Text Solution
|
- Initially capacitor is uncharged at t = 0 switch is closed. Charge on ...
Text Solution
|
- In circuit shown in figure charge on capacitor is Q = 100muC . If swit...
Text Solution
|
- A charged capacitro and an inductor are connected in series. At time t...
Text Solution
|