A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
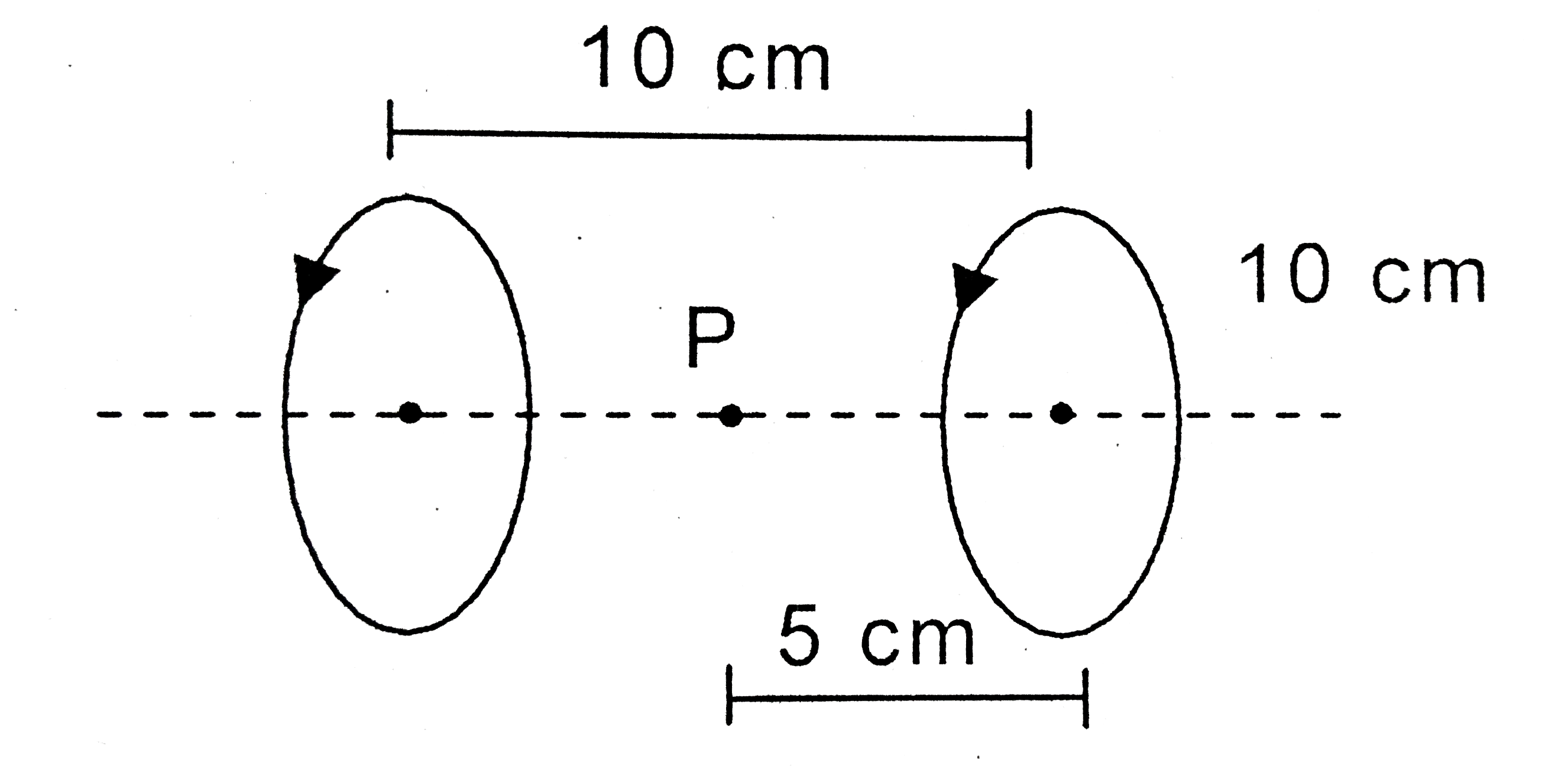
- Two circular loops having same radius [ R = 10 cm] and same current (7...
Text Solution
|
- 100 टेस्ला (T) के चुंबकीय क्षेत्र के लंबवत एक तल में एक तार 10 सेमी त्...
Text Solution
|
- Two circular loops having same radius [ R = 10 cm] and same current (7...
Text Solution
|
- A circular loop of radius 3 cm is having a current of 12.5 A. The magn...
Text Solution
|
- A circular wire loop of radius 30 cm carries a current of 3.5 A. Find ...
Text Solution
|
- The magnetic field due to a current carrying circular loop of radius 6...
Text Solution
|
- The magnetic field due to a current carrying circular loop of radius 3...
Text Solution
|
- The magnetic field due to current carrying circular coil loop of radiu...
Text Solution
|
- Two small homogeneous circular loops with traces (1) and (2), in which...
Text Solution
|