Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
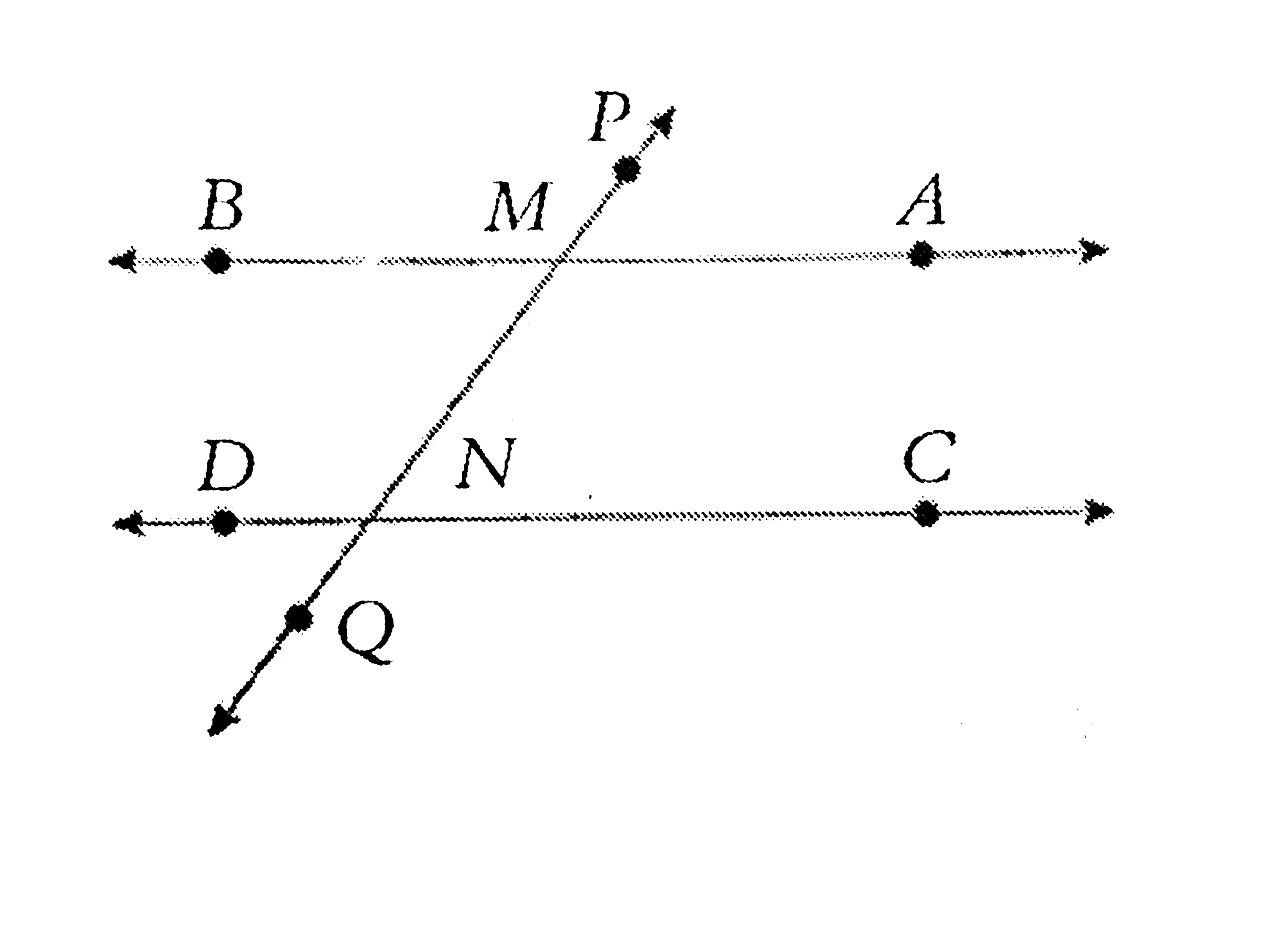
- In the figure above, bar(BA) is parallel to bar(DC), and bar(PQ) is a ...
Text Solution
|
- In the figure given below, bar(ED)||bar(AB) and bar(EF)||bar(BC) . If ...
Text Solution
|
- In the figure below, bar(AB)||bar(FC),bar(AE)||bar(BC) and bar(AF)||ba...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- In the figure above, bar(PQ) and bar(RS) are parallel. bar(AC) is tran...
Text Solution
|
- In the figure above, bar(BA) is parallel to bar(DC), and bar(PQ) is a ...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- In the following figure, if O is the center of the circle and bar(AB) ...
Text Solution
|
- In the following figure, bar(BD) is produced to E. If bar(AD) is the a...
Text Solution
|