Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MENSURATION
PEARSON IIT JEE FOUNDATION|Exercise Concept Application (Level 1 )|30 VideosMENSURATION
PEARSON IIT JEE FOUNDATION|Exercise Concept Application (Level 2 )|22 VideosMENSURATION
PEARSON IIT JEE FOUNDATION|Exercise Test Your Concepts (Short Answer Type Question )|15 VideosMATRICS
PEARSON IIT JEE FOUNDATION|Exercise Concept Application Level 2 |15 VideosMOCK TEST PAPER
PEARSON IIT JEE FOUNDATION|Exercise Questions|5 Videos
Similar Questions
Explore conceptually related problems
PEARSON IIT JEE FOUNDATION-MENSURATION-Test Your Concepts (Eassy Type Question )
- A conical tent is 48 m high and the diameter of its base is 28 m. The ...
Text Solution
|
- From a square metal sheet of side 5 cm , three circular plates of radi...
Text Solution
|
- In the figure given below, the area of the shaded region is 44 cm^2. O...
Text Solution
|
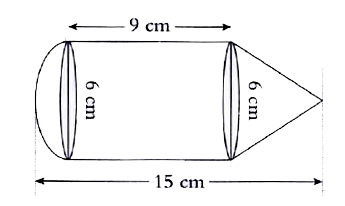
- In the above figure , a solid consisting of a cylinder surmounted by a...
Text Solution
|
- A hollow sphere which has internal and exter-nal diameters as 14 cm an...
Text Solution
|