Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
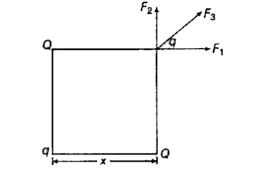
- The opposite corners of square carry Q charges each and the other two ...
Text Solution
|
- A charge Q is place at each of the opposite corners of a square. A cha...
Text Solution
|
- A charges Q is placed at each of the two opposite corners of a square....
Text Solution
|
- Charges Q-q, Q,-q are placed at the corners A, B, C,D of a square res...
Text Solution
|
- A charge +q is fixed to each of three corners of a square .On the empt...
Text Solution
|
- एक वर्ग के दो विपरीत कोनो में से प्रत्येक पर आवेश Q है। शेष दो कोनो मे...
Text Solution
|
- एक वर्ग के दो विपरीत कोनों पर आवेश Q रखा है तथा शेष दो कोनों पर आवेश q...
Text Solution
|
- A charge Q is placed at each of the opposite corners of square. A char...
Text Solution
|
- दो समान बिन्दु आवेश Q=+sqrt(2)muC एक वर्ग के दो विपरीत कोनो पर रखे जा...
Text Solution
|