Let the centre of the square be at O. The charge placed on the centre is ` 1 muC `
` AB = BC = CD = DA = 10 cm `
` AC = sqrt2 xx 10 = 10 sqrt2 cm `
` AC = BD = 10 sqrt2 cm `
` AO = BO = CO = DO = (10 sqrt2)/(2 ) = 5 sqrt2 cm `
Let the force on charge ` 1 mu C ` due to ` q_A " be " F_A ` which is directed away from both charges ` q_A and q ` (because both charges are positive in nature , so they will repel each other. )
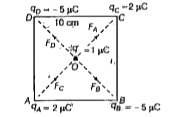
The force on charge ` 1 mu C ` due to ` q_B ` is ` F_B ` which is towards `q_B ` (because `q_B` is negatively charged and q is positively charged so they will attract each other) The force on charge ` 1 mu C ` due to ` q_C " is " F_C ` , which is directed away from both ` q_C and q` (as they both are positive in nature so will repel each other) . The force on charge ` 1 mu C ` due to ` q_D " is " F_D` , which is towards `q_D ` ( because ` q_D ` is negatively charged and q is positively charged , so they will attract each other.)
Force between q and `q_A`
` F_A = (1)/(4piin _0) . (| qqA|)/((OA)^(2)) = ( 9xx 10 ^(9) xx 1 xx 10 ^(-6) xx 2 xx 10 ^(-6))/((5sqrt2 xx 10 ^(-2) )^(2)) `
` = (9xx 2 xx 10 ^(-3))/(25 xx 2 xx 10 ^(_4)) = (90 )/(25) = (18)/(5)`
` F_A = 3.6N ` " " (direction towards O to C) Force between q and `q_B `
` F_B = (1)/(4 piin _0) . (| qq_B|)/((OB)^(2)) `
` " " = 9.0 N " " ` (direction towards O to B ) Force between q and ` q_C `
` F_C = (1)/(4piin _0) . (| qq _C|)/((OC)^(2)) = (9 xx 10 ^(9) xx1 xx 10 ^(-6) xx 2 xx 10 ^(-6))/((5sqrt2xx 10 ^(-2))^(2) )`
` F_C = ( 90 )/(25) = (18)/(5) = 3.6N ` ( direction towards O to A)
Here we observe that `F_A and F_C ` are of same magnitude and opposite in direction . so the resultant force of `F_A and F_C ` is zero.
Force between q and ` q_D `
` F_D = ( 1 )/(4piin _0) . (|qq_D|)/((OD) ^(2))`
`= ( 9 xx 10^(-6) xx 5 xx 10^(-6))/((5sqrt2xx10 ^(-2))^(2)) `
` F_D = 2.25 N " " ` (direction towards O to D)
Here, we observe that ` F_B and F_D ` are of same magnitude and opposite in direction . so that resultant force of ` F_D and F_B ` is zero.
Thus, the net resultant force on ` 1 muC ` (placed at O) is zero, as all the force balance each other.
