Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
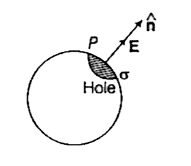
- Electric Field in the Hole of a Charged Conductor A hollw charged co...
Text Solution
|
- A hollow charged conductor has a tiny hole cut into its surface. Sho...
Text Solution
|
- एक खोखले आवेशित गोले की सतह पर एक छोटा छिद्र काटा गया है। सिद्ध करो की...
Text Solution
|
- A hollow charged conductor has a tiny hole cut into its surface. Show ...
Text Solution
|
- A hollow charged conductor has a tiny hole cut into its surface. Show ...
Text Solution
|
- Show that electric field intensity on the surface of a charged conduct...
Text Solution
|
- A hollow charged conductor has a tiny hole cut into its surface. Sho...
Text Solution
|
- A hollow charged conductor has a tiny hole cut in to its surface show ...
Text Solution
|
- A hollow charged conductor has a tiny hole cut in to its surface show ...
Text Solution
|