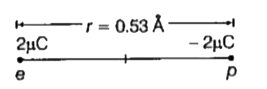Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Electrostatic Potential Energy of a system of Two Point Charges In a...
Text Solution
|
- In a hydrogen atom, the electron and proton are bound together at a di...
Text Solution
|
- In a hydrogen atom, the electron and proton are bound at a distance of...
Text Solution
|
- एक हाइड्रोजन परमाणु में इलेक्ट्रॉन तथा प्रोटॉन लगभग 0.53 Å दुरी पर पर...
Text Solution
|
- In a hydrogen atom , the electron and proton are bound at a distance o...
Text Solution
|
- In a hydrogen atom, the electron and proton are bound at a distance of...
Text Solution
|
- In a hydrogen atom, the electron and proton are bound at a distance of...
Text Solution
|
- The potential energy of a system increases, if work is done
Text Solution
|
- In a hydrogen atom, the electron and proton are bound at a distance of...
Text Solution
|