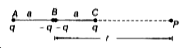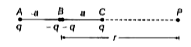Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Given fgure shows a charge array known as an electric quadrupole. For ...
Text Solution
|
- Fig shows a charge array known as an 'electric quadrupole'. For a poin...
Text Solution
|
- Figure shows a charge array known as an "electric quadrupole". For a p...
Text Solution
|
- नीचे दिए गए चित्र 2.32 में के आवेश विन्यास जिसे विद्युत चतुर्ध्रुवी कह...
Text Solution
|
- निम्न चित्र में एक आवेश विन्यास जिसे विद्युत चतुर्ध्रुवी कहा जाता है, ...
Text Solution
|
- चित्र में प्रदर्शित चार आवेशों का संयुक्त निकाय विधुत-चतुध्रुव (electr...
Text Solution
|
- Electric potential (phi) of a quadrupole varies with distance 'r' on i...
Text Solution
|
- Three charged particles having charges q, -2q & q are placed in a line...
Text Solution
|
- The figure given below shows a charge array known as an 'electric quad...
Text Solution
|