Home
Class 12
CHEMISTRY
The arrangement of X^(ɵ) ions around A^(...

The arrangement of `X^(ɵ)` ions around `A^(o+)` ion in solid `AX` is given in the figure (not drawn to scale). If the radius of `X^(ɵ)` is `180 pm`, the radius of `A^(o+)` is

A

104 pm

B

125 pm

C

183 pm

D

75 pm

Text Solution

Verified by Experts

The correct Answer is:
A
According to the given figure. `A^(+)` is present in the octahedral void of `X^(-)` The limiting radius in octahedral void is related to the radius of sphere as
`r_("void")=0.414 " sphere"`
`r_(A)=0.414r`
`=0.414xx250 "pm"=103.5`
`=104 "pm"`
Promotional Banner

Similar Questions

Explore conceptually related problems

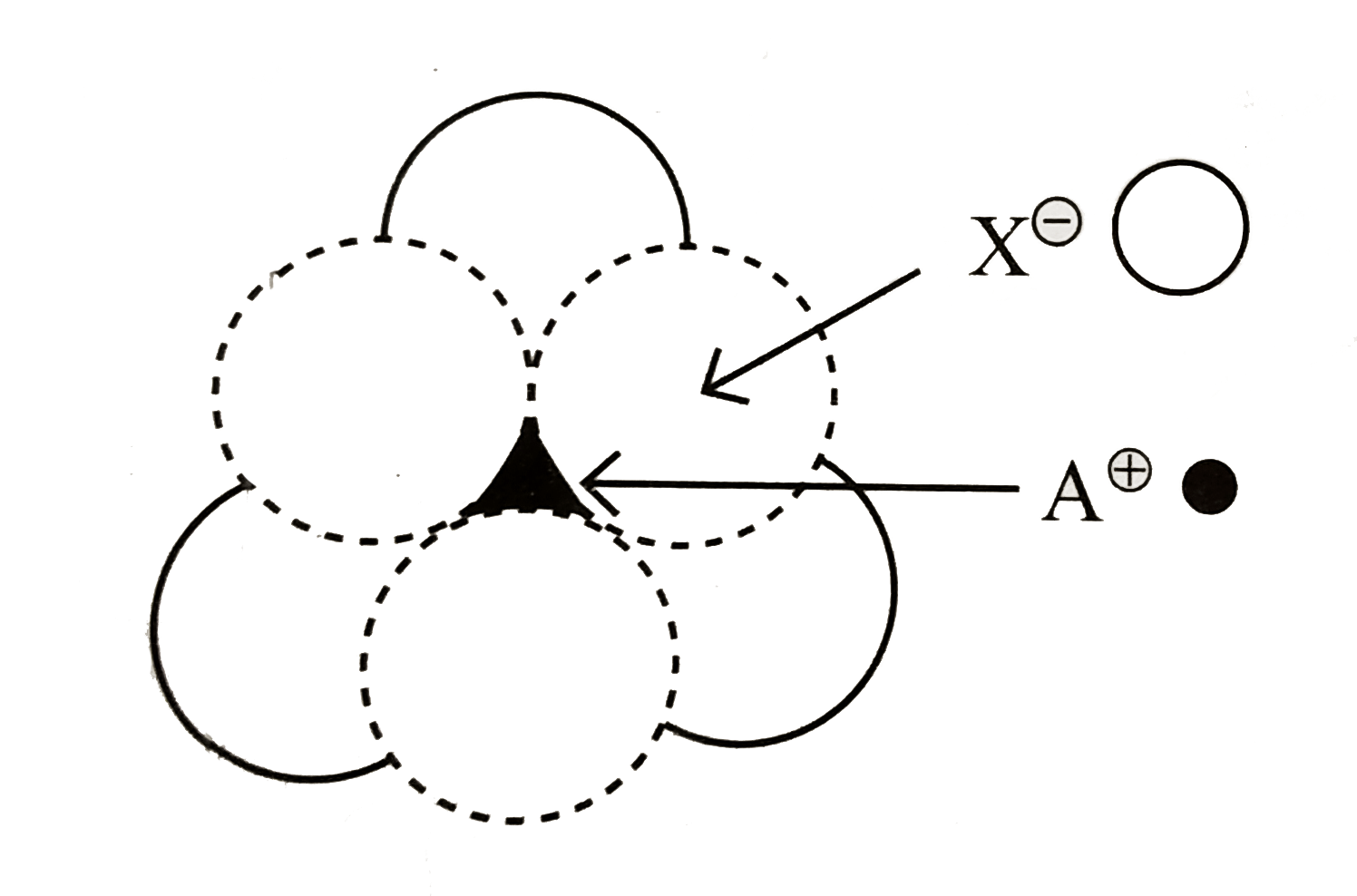
The arrangement of X^(ɵ) ions around A^(o+) ion in solid AX is given in the figure (not drawn to scale). If the radius of X^(ɵ) is 250 pm , the radius of A^(o+) is

A solid XY has NaCl structure. If radius of X^(+) is 100 p m . What is the radius of Y^(-) ion ?

A solid AB has ZnS-type structure. The edge lenth of unit cell is 400 pm abd the radius of 'B^-' ion is 0.130 nm. Then the radius of 'A^+' ion is

NH_(4) X1 crystallizes in bcc lattice with edge length 383 pm. If the radius of NH_(4)^(+) ion is 154 pm ,calculate the radius of halide (X^(-) ) .

An ionic solid A^(o+)B^(Θ) crystallizes as an fcc structure. If the edge length of cell is 508 pm and the radius of anion is 144 pm , the radius of cation is

Cesium chloride forms a body-centred cubic lattice. Cesiumm and chloride ions are in contact along the body diagoanl of a cell. The length of the side of the unit cell is 412 pm and Cl^(Θ) ion has a radius of 181 pm. Calculate the radius of Cs^(o+) ion.

In the given figure, O is the centre of the circle with radius 14 cm. Find the area of the shared portion

Casium may be considered to form interpentrating simple primitice cubic crystal. The edge length of unit cell is 412 pm. Determine a. The density of CsCl . b. The inoic radius of Cs^(o+) if the ionic radius of Cl^(Θ) is 181 pm. Given: Aw (Cs) = 133 g mol^(-1)

The "OLIVINE" series of minerals consists of crystal in which Fe^(2+) and Mg^(2+) ions may substitute for each other causing susbstitutional impurity defects without changing the volume of unit cell. In "OLIVINE" series of minerals, O^(2-) ions exist as fcc with Si^(4+) occupying one-fourth of OVs and divalent metal ions occupying one-fourth of OVs and divalent metal ions occupying one-fourth of TVs . The density of "forsterite" (magnesium silicate) is 3.21 g cm^(-3) land that of "fayalite" (ferrous silicate) is 4.34 g cm^(-3) . If in "forsterite mineral" bivalent Mg^(2+) ions are to be replaced by unipositive Na^(o+) ions, and if Na^(o+) ions are occupying half of TV_(s) in fcc lattice, the arrangement of rest of the constituents is kept same, then the formula of the new solid is:

In an LiI crystal, I^(ɵ) ions from a cubical close-packed arrangement, a nd Li^(o+) ion occupy octahedral holes. What is the relationship between the edge length of the unit cells and radii of the I^(ɵ) ions if a = 60 "pm".