एक समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं |
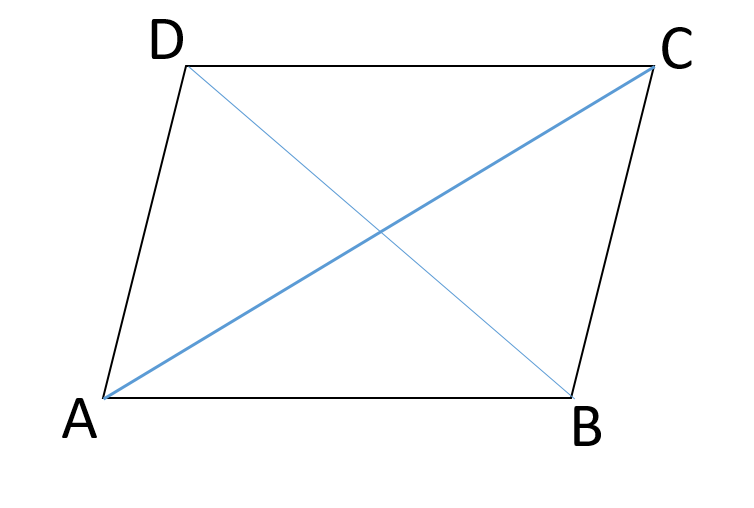
जैसा कि दिया गया है मान लिया कि ABCD एक समांतर चतुर्भुज है।
अत: DC || AB और AD || BC
[चूँकि समांतर चतुर्भुज में सम्मुख भुजाएँ समांतर होती हैं।]
अत: सिद्ध करना है कि,
`angleABC = angleCDA` और, `angleDAB = angleBCD`
बिंदु A और C तथा बिंदु D और B को मिलाया गया।
अतः `triangleACD` और `triangleABC` में,
AD || BC और AC एक तिर्यक रेखा हैँ जो इन दोनों समांतर रेखाओं को क्रमश: बिंदु A और बिंदु C पर काटती है।
हम जानते हैं कि यदि एक तिर्यक रेखा दो समांतर रेखाओं को काटती है तो एकांतर अंत: कोणों का प्रत्येक युग्म बराबर होता है।
यहाँ `angleDAC` और `angleBCA` एकांतर अंत: कोणों का युग्म है, अत: आपस में बराबर हैं।
अर्थात `angleDAC = angleBCA`
उसी प्रकार `angleCAB` और `angleACD` एकांतर अंत: कोणों का युग्म है, अत: आपस में बराबर हैं।
अत: `angleCAB = angleACD`
और भुजा AC दोनों त्रिभुजों में उभयनिष्ठ (कॉमन) है।
यहाँ दो कोण और उन दोनों कोणों के बीच की भुजा आपस में बराबर है।
अत: ASA (कोण भुजा कोण) सर्वांगसमता नियम से
`ΔACD CONG ΔABC`
अत: CPCT के अनुसार हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं
`angleABC = angleCDA` - - - - - (i)
उसी प्रकार `triangleABD` और `triangleBCD` में,
DC||AB
और एक तिर्यक रेखा DB दोनों समांतर रेखाओं DC और AB काटती है अत: इस प्रकार बने हुए एकांतर अंत: कोणों के युग्म बराबर होंगे।
अत: `angleABD = angleBDC`
और, `angleCDA = triangleDBC`
और भुजा DB दोनों त्रिभुजों ABD और BCD में उभयनिष्ठ (कॉमन) है।
अत: ASA (कोण भुजा कोण) सर्वांगसमता नियम से,
`triangleABD cong triangleBCD`
अब CPCT के अनुसार हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं
`angleDAB = angleBCD` - - - - - (ii)
अब समीकरण (i) और समीकरण (ii) से
`angleABC = angleCDA` और `angleDAB = angleBCD` प्रमाणित
अत: एक समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं।
