लिखित उत्तर
Verified by Experts
Recommended Questions
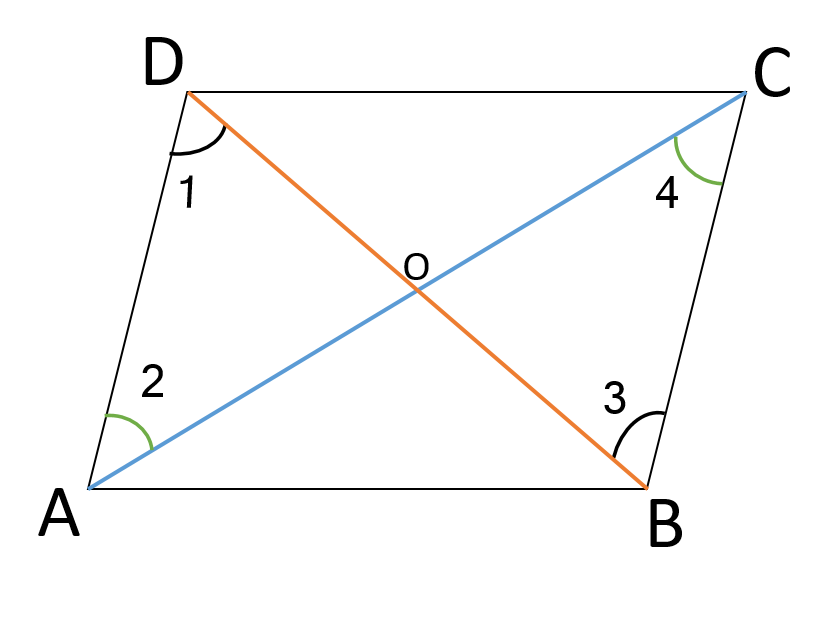
- सिद्ध कीजिए : समांतर चतुर्भुज के विकर्ण एक दूसरे को (परस्पर) समद्विभाज...
Text Solution
|
- सिद्ध कीजिये की बिंदु (1,-2) ,(3,6),(5,10) और (3,2) एक समांतर चतुर्भु...
Text Solution
|
- यदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित कर...
Text Solution
|
- सिद्ध कीजिए कि y^(2)+2ax+2by+c=0 एक परवलय को निरूपित करता है जिसका अ...
Text Solution
|
- यदि |veca+vecb|=|vecb|, तो सिद्ध कीजिए कि veca और veca+2vecb परस्पर लम...
Text Solution
|
- एक समान्तर चतुर्भुज की दो आसान भुजाएँ 2hati-4hatj-5hatk और 2hati+2hat...
Text Solution
|
- सिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसर...
Text Solution
|
- Revision|समांतर चतुर्भुज के गुण
Text Solution
|
- चुम्बक के समान ध्रुव एक दूसरे को
Text Solution
|