Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-RELATIONS AND FUNCTIONS-All Questions
- If f(x) is a real-valued function defined as f(x)=In (1-sinx), then t...
Text Solution
|
- Find the range of f(x)=cos((log)e{x})dot
Text Solution
|
- Plot y=sinxa n dy=2sinxdot
Text Solution
|
- If f:x->y, where x and y are sets containing natural numbers, f(x)=(x...
Text Solution
|
- Find the domain and range of f(x)=cos^(-1)sqrt((log)([x])((|x|)/x))
Text Solution
|
- Discuss the continuity of the following function : f(x)={1,ifxi sr a t...
Text Solution
|
- Find the range of f(x)=(log)([x-1])sinxdot
Text Solution
|
- Plot y=sinxa n dy=sin(x/2)
Text Solution
|
- The function f(x) is defined on the interval [0.1] Then match the foll...
Text Solution
|
- In the questions, [x]a n d{x} represent the greatest integer function ...
Text Solution
|
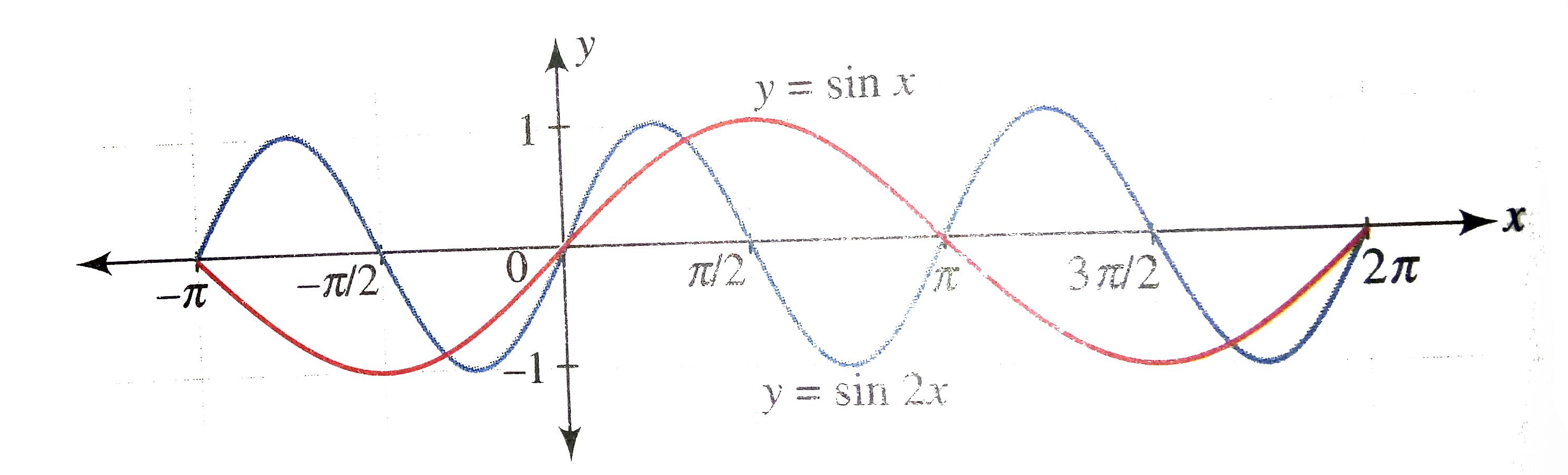
- Plot y=sinxa n dy=sin2xdot
Text Solution
|
- Let f(x)=x+2|x+1|+2|x-1|dot If f(x)=k has exactly one real solution, ...
Text Solution
|
- Sketch the curve y="log"|x|
Text Solution
|
- Find the domain of (a)f(x)=1/(sqrt(x-[x])) (b) f(x)=1/(log[x]) (c)f...
Text Solution
|
- The domain of f(x)=sin^(-1)[2x^2-3],w h e r e[dot] denotes the greates...
Text Solution
|
- Find the domain of f(x)=1/(sqrt(|[|x|-1]|-5))
Text Solution
|
- Sketch the graph for y=|sinx|dot
Text Solution
|
- Match the column Column I (Function), Column II (Period) p. f(x)=si...
Text Solution
|
- Draw the graph for y=|logx|
Text Solution
|
- Find the domain of f(x)=1/(sqrt(|[|x|-1]|-5))
Text Solution
|