Text Solution
Verified by Experts
Topper's Solved these Questions
MATHMETICAL REASONING
CENGAGE PUBLICATION|Exercise concept application|13 VideosMATHMETICAL REASONING
CENGAGE PUBLICATION|Exercise Single correct answer type|38 VideosLOGARITHM AND ITS PROPERTIES
CENGAGE PUBLICATION|Exercise JEE ADVANCED|1 VideosMATRICES
CENGAGE PUBLICATION|Exercise All Questions|509 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-MATHMETICAL REASONING-Archives
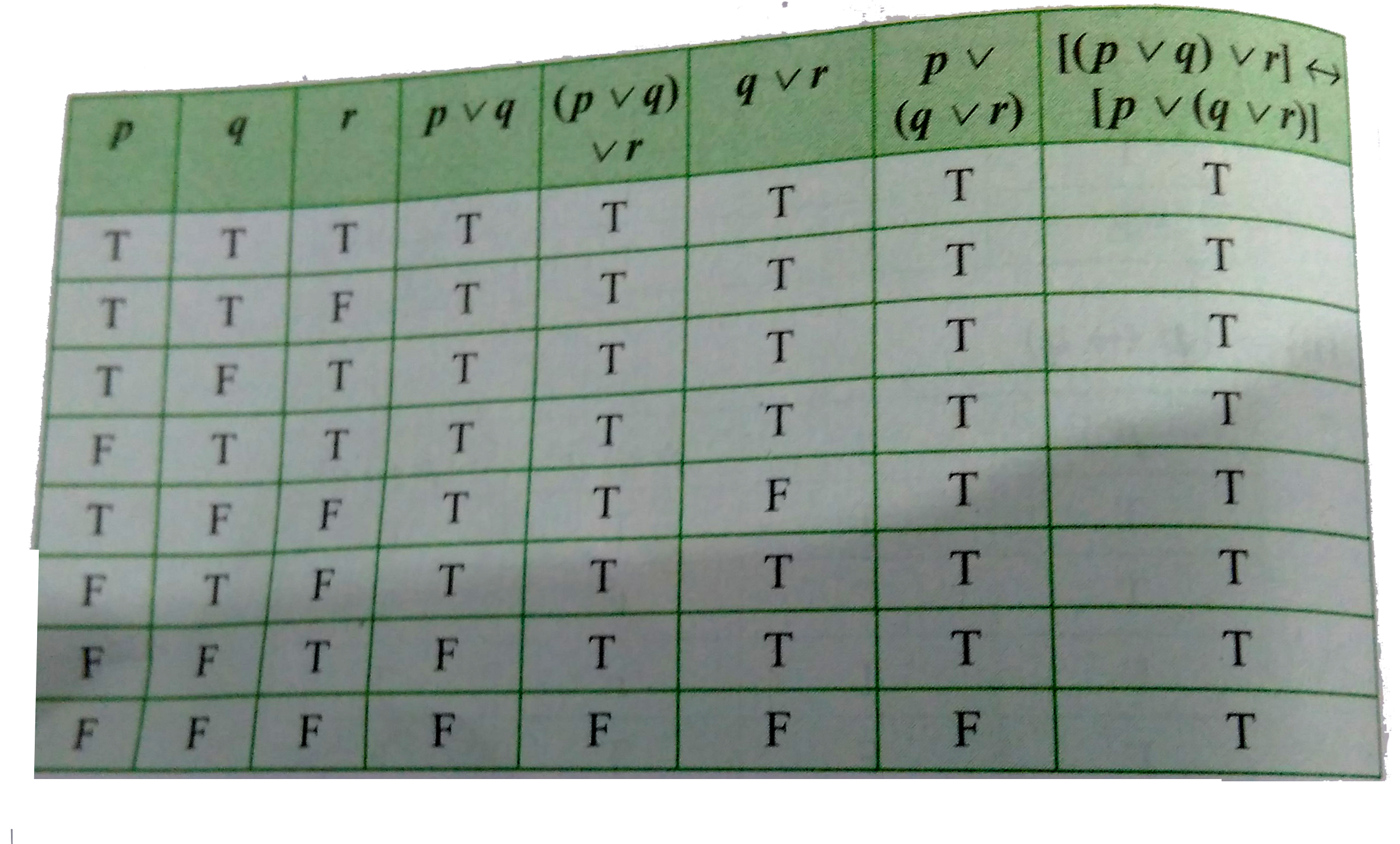
- Show that [(pvvq)vvr] harr [pvv(qvvr)] is a tautology
Text Solution
|
- Statements -1 : ~(pharr~q) is equivalent to p harr q Statement-2: ~(...
Text Solution
|
- If S be a non - empty subset of R. Consider the following statement ...
Text Solution
|
- Consider the following statements P: Suman is brilliant Q: Suman i...
Text Solution
|
- The negation of the statement "If I become teacher, then I will open ...
Text Solution
|
- Statement I : (p^^∼q)∧(∼p^^q) is a fallacy. Statement II : (p→q)↔(∼q→...
Text Solution
|
- The statement ~(pharr~q) is
Text Solution
|
- The negation of ~svv(~r^^s) is equivalent to
Text Solution
|
- The Boolean Expression (p^^~ q)vvqvv(~ p^^q) is equivalent to : (1) ~...
Text Solution
|
- The following statement (p to q) to [(~p to q) to q] is
Text Solution
|
- The Boolean expression (p wedge r) rarr (p vee r) is equivalent to
Text Solution
|