Home
Class 12
MATHS
Show that (p^^q)vv(~p)vv(p^^~q) is a tau...

Show that `(p^^q)vv(~p)vv(p^^~q)` is a tautology

Text Solution

Verified by Experts


fol all possible truth values of p and q, the compound statement
`(p^^q)vv(~p)vv(p^^~q)` is true.
Thus, `(p^^q) vv(~p)vv(p^^~q)` is a tautology .
Promotional Banner

Topper's Solved these Questions

  • MATHMETICAL REASONING

    CENGAGE PUBLICATION|Exercise Single correct answer type|38 Videos

  • MATHMETICAL REASONING

    CENGAGE PUBLICATION|Exercise Archives|10 Videos

  • MATHMETICAL REASONING

    CENGAGE PUBLICATION|Exercise Archives|10 Videos

  • LOGARITHM AND ITS PROPERTIES

    CENGAGE PUBLICATION|Exercise JEE ADVANCED|1 Videos

  • MATRICES

    CENGAGE PUBLICATION|Exercise All Questions|509 Videos

Similar Questions

Explore conceptually related problems

Prove that the statement - ~(pharr q) harr {(p^^~q) vv (~p^^q)} is a tautology.

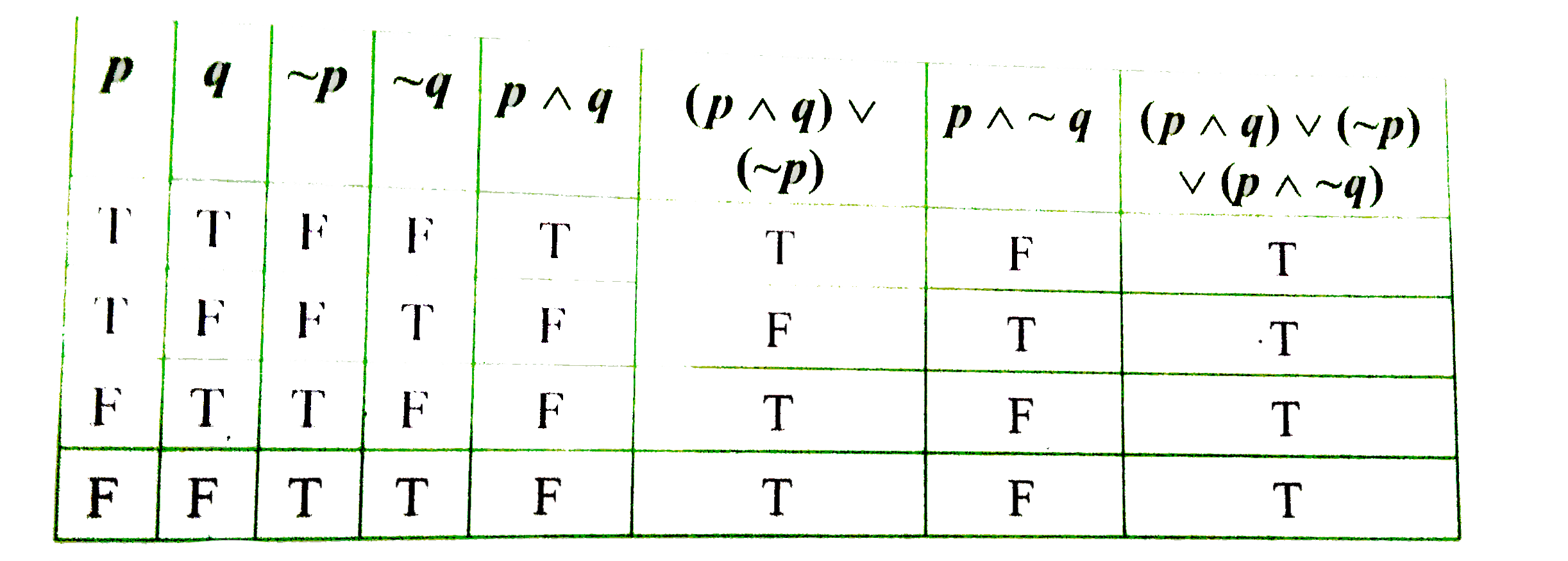
Show that (i) p to (pvvq) is a tautology (ii) (pvvq) ^^(~ p ^^~q) is a contradiction

(p^^~q)^^(~p^^q) is

consider : Statement - I : (p^^~q)^^(~p^^q) is a fallacy . Statement -II : (prarrq)harr(~qrarr~p) is a tautology .

Show that [(ptoq)^^(qto r)] to ( p to r) is a tautology

Prove that [(p^^~q)vv(q^^~p)]^^(pvvq)=(pvvq)^^(~qvv~p)^^(pvvq)

Statement I : (p^^∼q)∧(∼p^^q) is a fallacy. Statement II : (p→q)↔(∼q→∼p) is a tautology.

Statements -1 : ~(pharr~q) is equivalent to p harr q Statement-2: ~( p harr ~q) is a tautology.

The Boolean Expression (p^^~ q)vvqvv(~ p^^q) is equivalent to : (1) ~ p^^q (2) p^^q (3) pvvq (4) pvv~ q

(~(pvvq))vv(~p^^q) is logically equivalent to