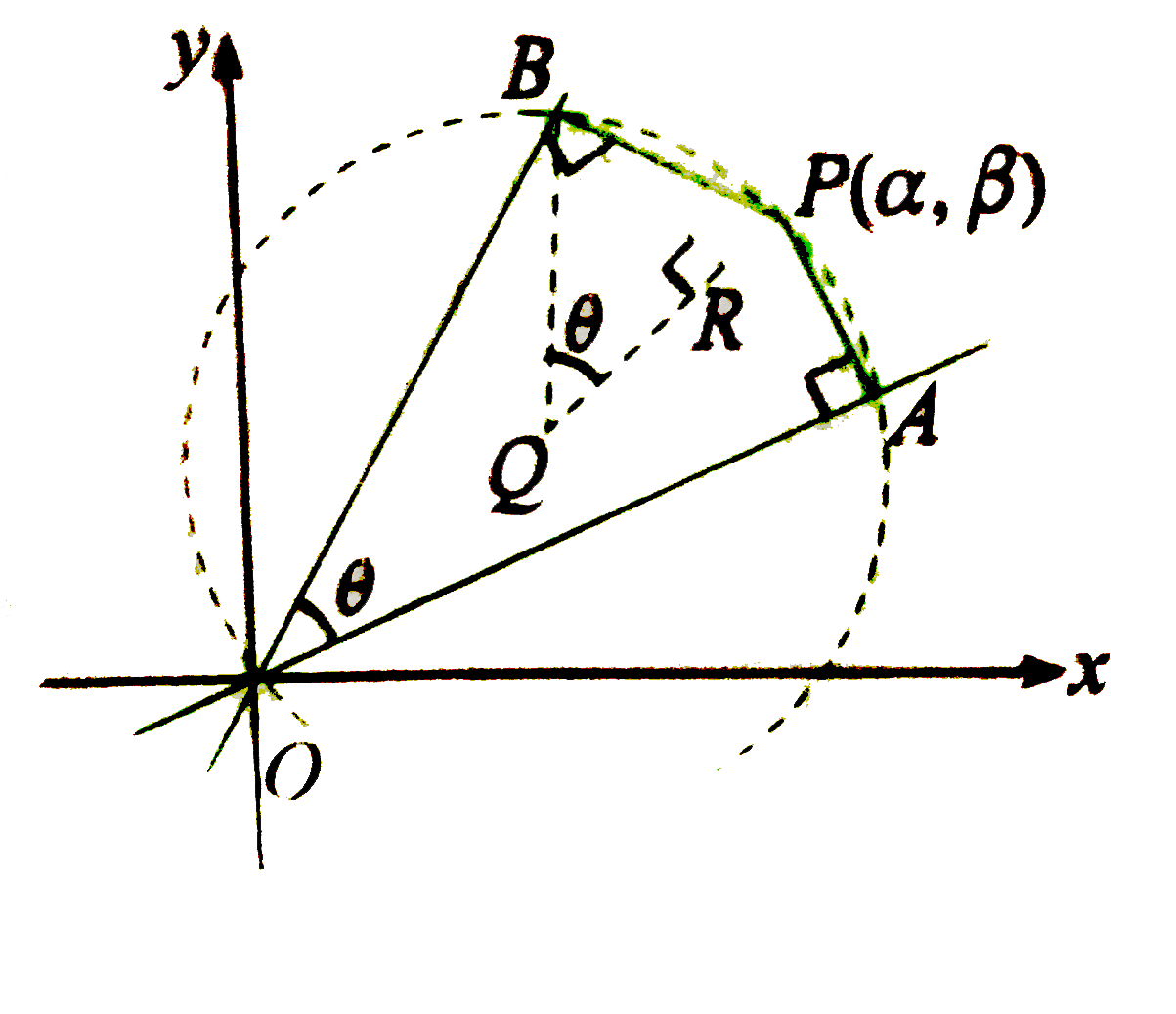Home
Class 12
MATHS
A point moves so that the distance betwe...

A point moves so that the distance between the foot of perpendiculars from it on the lines `a x^2+2hx y+b y^2=0` is a constant `2d` . Show that the equation to its locus is `(x^2+y^2)(h^2-a b)=d^2{(a-b)^2+4h^2}dot`

Text Solution

Verified by Experts


From point `p(alpha , beta),` perpendiculars are dropped on the given pair of lines.
According to the question , AB=2d. Clearly OAPB is a cyclic quadrilateral and OP will be the diameter of the circumcircle of this quadrilateral.
`OP =sqrt(alpha^(2)+ beta^(2))`
Let Q be the center of the circle.
therefore , in `DeltaQRB`,
`sintheta=(BR)/(QB)=(2d)/(sqrt(alpha^(2)+beta^(2)))` (1)
Also , angle between the lines is
`tantheta=(2sqrt(h^(2)-b))/(a+b)` (2)
Therefore , from (1) and (2), we get
`(2sqrt(h^(2)-ab))/(a+b)=(2d)/(sqrt(alpha^(2)+beta^(2)-4d^(2)))`
Therefore , the locus of `P(alpha,beta)`is
`(x^(2)+y^(2))(h^(2)-ab)=d^(2){(a-b)^(2)4h^(2)}`
Promotional Banner

Topper's Solved these Questions

  • PAIR OF STRAIGHT LINES

    CENGAGE PUBLICATION|Exercise Exercise 3.1|6 Videos

  • PAIR OF STRAIGHT LINES

    CENGAGE PUBLICATION|Exercise Exercise 3.2|7 Videos

  • PAIR OF STRAIGHT LINES

    CENGAGE PUBLICATION|Exercise Illustration 3.17|1 Videos

  • MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS

    CENGAGE PUBLICATION|Exercise Comprehension Type|6 Videos

  • PARABOLA

    CENGAGE PUBLICATION|Exercise Matching Column Type|1 Videos

Similar Questions

Explore conceptually related problems

Find the foot of perpendicular drawn from the point (2, 2) to the line 3x - 4y + 5 = 0

The product of the perpendiculars from origin to the pair of lines a x^2+2h x y+b y^2 + 2gx + 2fy + c =0 is

The coordinates of the foot of the perpendicular drawn from the origin upon a line are (h,k) , show that the equation of the line is hx+ky=h^(2)+k^(2)(h^(2)+k^(2)ne0) .

The straight lines joining any point P on the parabola y^2=4a x to the vertex and perpendicular from the focus to the tangent at P intersect at Rdot Then the equation of the locus of R is (a) x^2+2y^2-a x=0 (b) 2x^2+y^2-2a x=0 (c) 2x^2+2y^2-a y=0 (d) 2x^2+y^2-2a y=0

A point P moves such that the chord of contact of the pair of tangents from P on the parabola y^2=4a x touches the rectangular hyperbola x^2-y^2=c^2dot Show that the locus of P is the ellipse (x^2)/(c^2)+(y^2)/((2a)^2)=1.

Prove that the product of the lengths of the perpendiculars drawn from the points (sqrt(a^2-b^2),0) and (-sqrt(a^2-b^2),0) to the line x/a costheta + y/b sintheta=1 is b^2 .

If one of the lines denoted by the line pair a x^2+2h x y+b y^2=0 bisects the angle between the coordinate axes, then prove that (a+b)^2=4h^2

P( h, k) is the mid-point of a line segment between axes. Show that equation of the line is x/a + y/b = 2 .

A point moves on a plane in such a manner that the difference of distance from (3,0) is (3)/(2) times its distance from the line 3x - 4 = 0 , Show that the locus of the moving point is a hyperbola and the equation of its locus is 5x^(2) - 4y^(2) = 20 .

If the pair of lines a x^2+2h x y+b y^2+2gx+2fy+c=0 intersect on the y-axis, then prove that 2fgh=bg^2+c h^2