Home
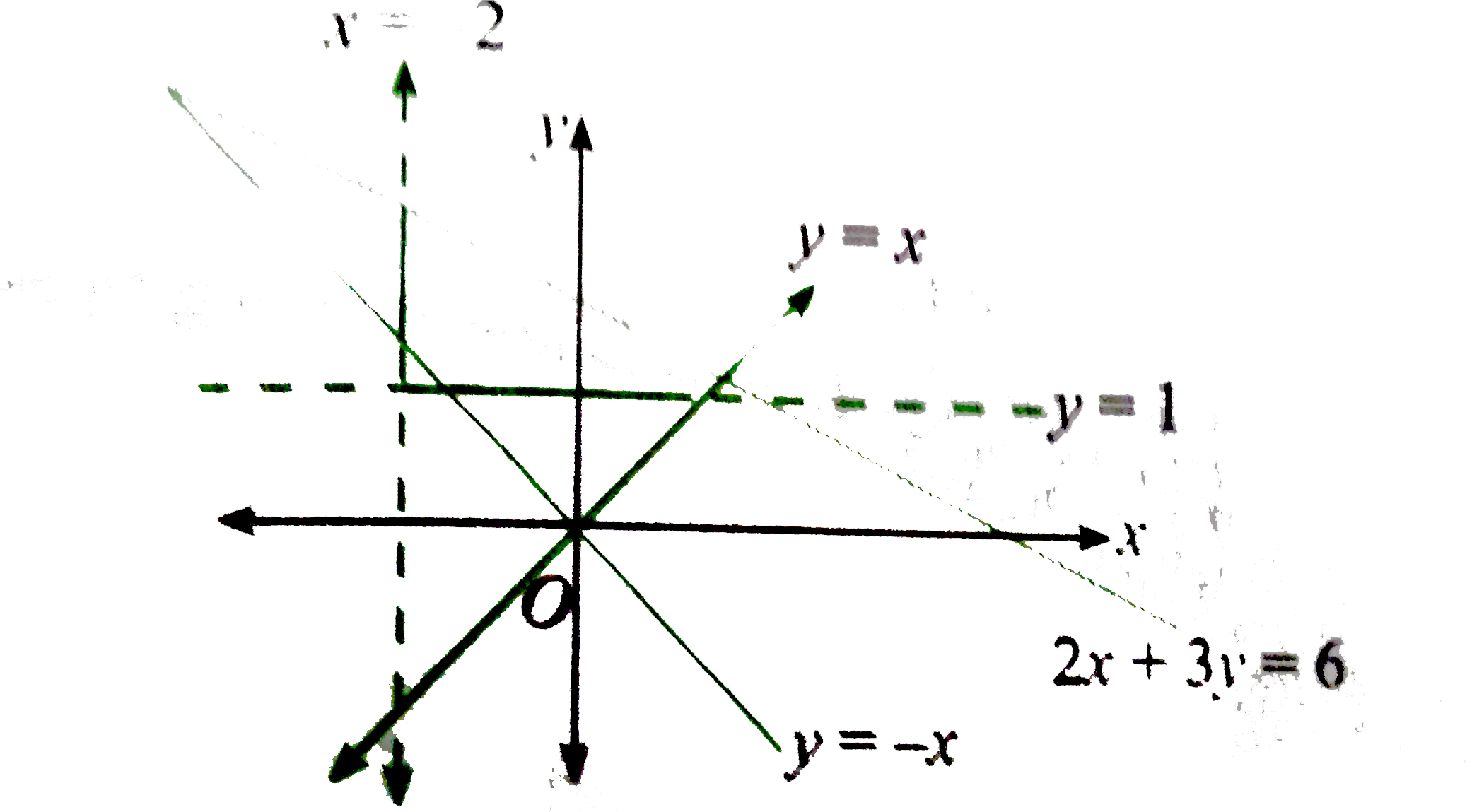
Class 12
MATHS
The combined equation of three sides of ...

The combined equation of three sides of a triangle is `(x^2-y^2)(2x+3y-6)=0` if (-2,a) is an interior point and (b,1) is an exterior point of the triangle, then

A

`2ltalt10//3`

B

`-2ltalt10//3`

C

`-1ltblt9//2`

D

`-1ltblt1`

Text Solution

Verified by Experts

The correct Answer is:
1,4
The separate equations of the sides are `x-y=0,x+y=0and 2x+3y-6=0` . The point (-2,a) moves on the line `x=-2` and the point (b,1) moves on the line `y=1` . From the figure , the y- coordinates of the points of intersection of `x=-2` with `y=-xand2x+3y=6` given the range of values of a . The x - coordinates of the points of intersection of `y=1` with `y=-xand y=x` give the range of values of b.
Promotional Banner

Topper's Solved these Questions

  • PAIR OF STRAIGHT LINES

    CENGAGE PUBLICATION|Exercise Linked Comprehension Type|6 Videos

  • PAIR OF STRAIGHT LINES

    CENGAGE PUBLICATION|Exercise Numberical Value Type|5 Videos

  • PAIR OF STRAIGHT LINES

    CENGAGE PUBLICATION|Exercise Single Correct Answer type|23 Videos

  • MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS

    CENGAGE PUBLICATION|Exercise Comprehension Type|6 Videos

  • PARABOLA

    CENGAGE PUBLICATION|Exercise Matching Column Type|1 Videos

Similar Questions

Explore conceptually related problems

The equations of two sides of a triangle are 3x-2y+6=0\ a n d\ 4x+5y-20\ a n d\ the orthocentre is (1,1). Find the equation of the third side.

The equation of three sides of a triangle are x + 2y - 5 = 0, x +y = 6 and y + 2x-4 = 0. Find the co-ordinate of its ortho centre

The equation to the base of an equilateral triangle is 4x-3y+10=0 and its vertex is at (-2,-1), find the length of a side of the triangle.

The equation of circumcircle of an equilateral triangle is x^2+y^2+2gx+2fy+c=0 and one vertex of the triangle is (1,1).The equation of incircle of the triangle is

The equations of the sided of a triangle are x+y-5=0,x-y+1=0, and y-1=0 . Then the coordinates of the circumcentre are

The equations of two sides of a triangle are 3y-x-2=0a n dy+x-2=0. The third side, which is variable, always passes through the point (5,-1) . Find the range of the values of the slope of the third side, so that the origin is an interior point of the triangle.

If the equation of the base of an equilateral triangle is 2x - y=1 and the vertex is (-1,2), then the length of a side of the triangle is-

The equation to the base of an equilateral triangle is x+y=2and its vertex is at (2,-1) . Find the length of a side of the triangle.

The equation of the in-circle of an equilateral triangle is x^(2) + y^(2) + 2x - 4y - 8 = 0 , find the area of the equilateral triangle.