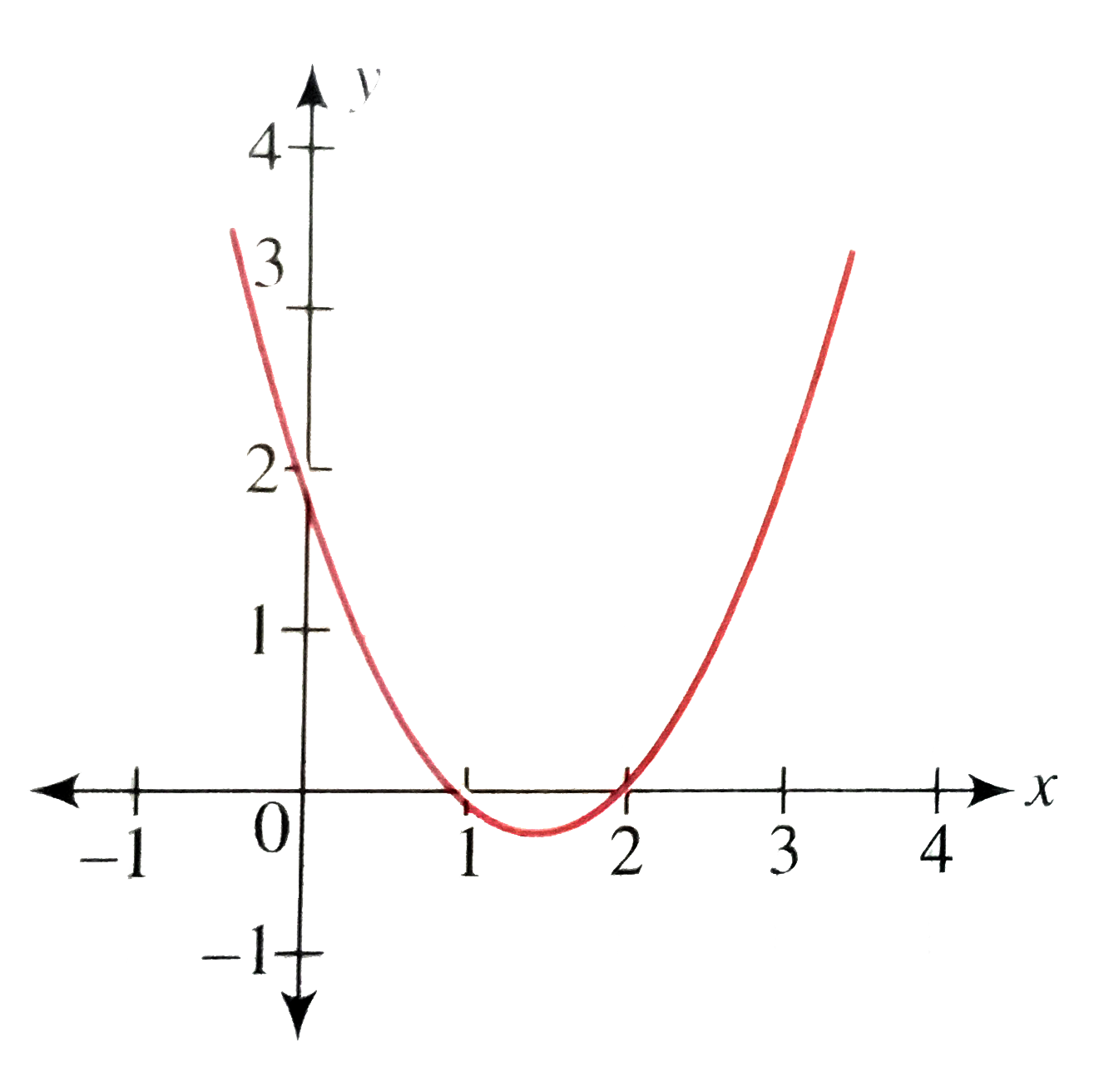
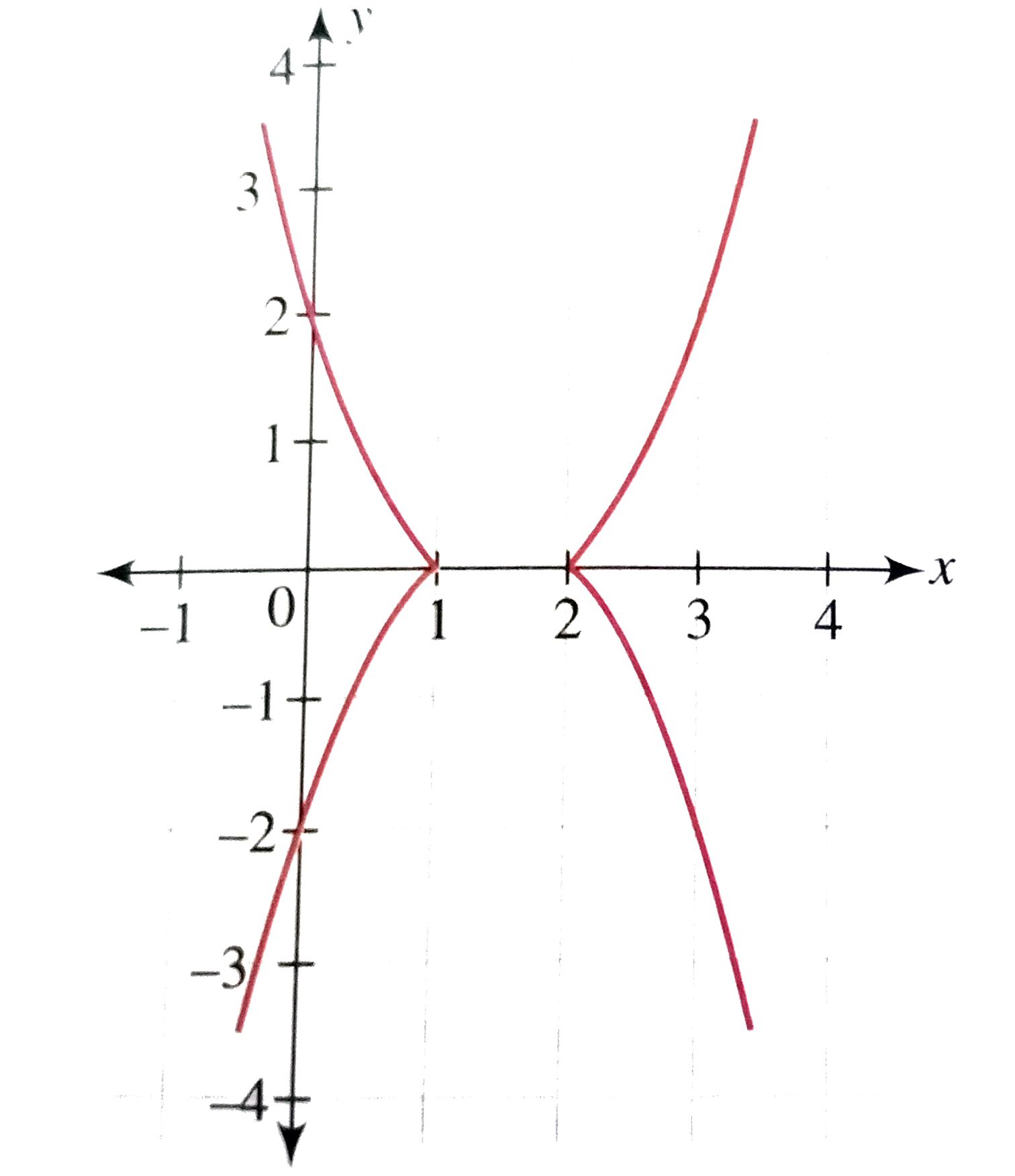
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-GRAPHICAL TRANSFORMATIONS-ILLUSTRATION
- Draw the graph of |y|=sinx.
Text Solution
|
- Draw the graph of |y|=tanx.
Text Solution
|
- Sketch the curve |y|=(x-1)(x-2)dot
Text Solution
|
- Draw the graph of |y|={x}, where {.} represents the fractional part fu...
Text Solution
|
- Draw the graph of |x|+|y|=1+x.
Text Solution
|
- Draw the graph of |x|-|y|=2 using graphical transformation.
Text Solution
|
- Draw the graph of y=|2^(|x|)-3|.
Text Solution
|
- The graph of the function y=f(x) is as shown in the figure. Then ...
Text Solution
|
- about to only mathematics
Text Solution
|
- Draw the graph and discuss the continuity of f(x)=[sinx+cosx],x in [0,...
Text Solution
|
- Draw the graph and find the points of discontinuity for f(x)=[x^(2)-x-...
Text Solution
|
- Draw the graph of y=tan^(-1)x+cot^(-1)x
Text Solution
|
- Draw the graph of y=|(1)/(|x|)-2|.
Text Solution
|
- Draw the graph of y=tan^(-1)x+cos^(-1)x+sin^(-1)x.
Text Solution
|
- Draw the graph of |y|=(x-1)(x-2)(x-3).
Text Solution
|
- Draw the graph of y=2sin^(-1)(x//3).
Text Solution
|
- Draw the graph of y=cot^(-1)(-x).
Text Solution
|
- Draw the graph of y=sec^(-1)|x|.
Text Solution
|
- Draw the graph of y=|log(e)(x+3)|.
Text Solution
|
- Draw the graph of y=|log(e)|x||.
Text Solution
|