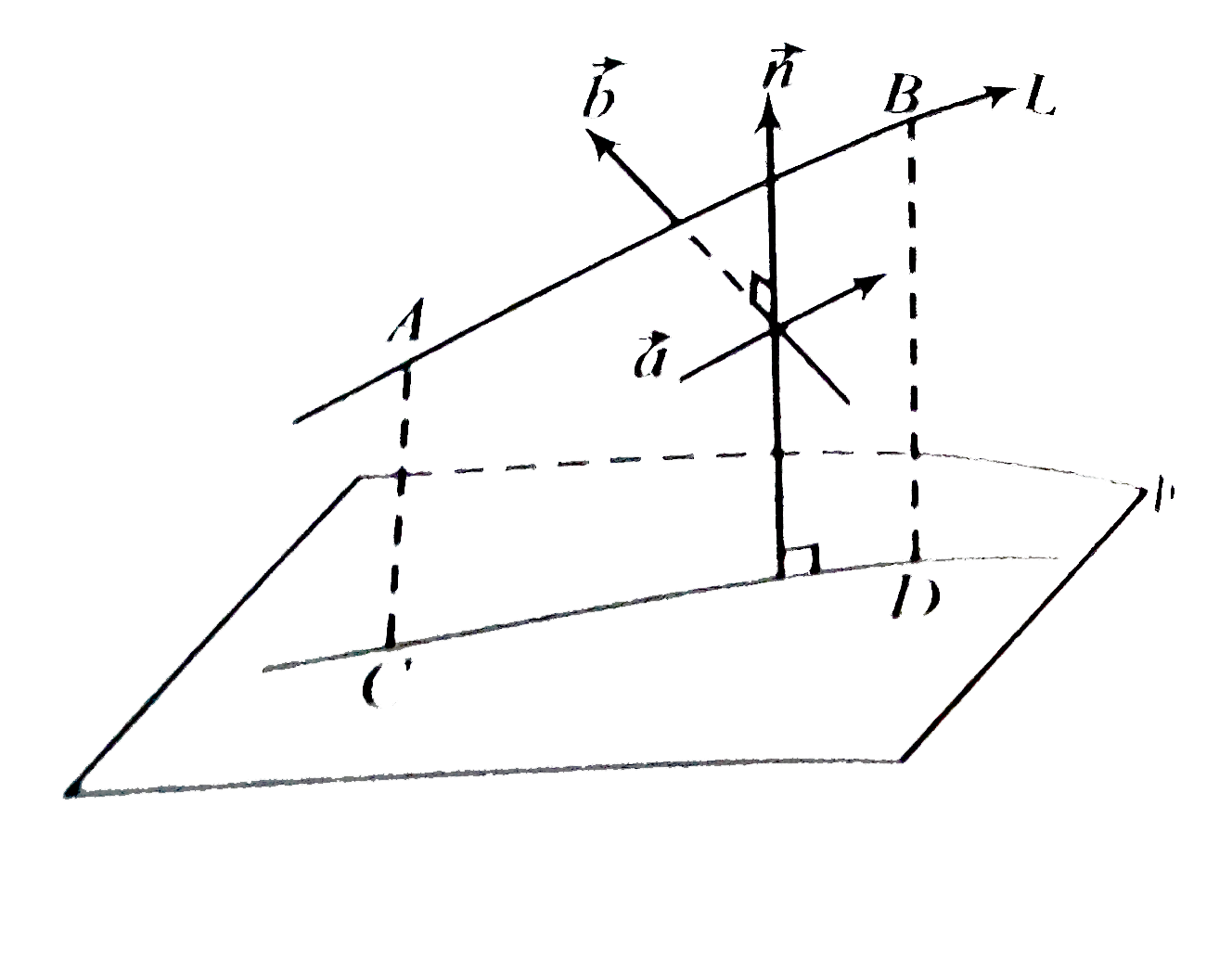
Text Solution
Verified by Experts
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 3.1|12 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 3.2|15 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise All Questions|291 VideosTRIGONOMETRIC EQUATIONS
CENGAGE PUBLICATION|Exercise Archives (Numerical value type)|4 Videos
Similar Questions
Explore conceptually related problems