Home
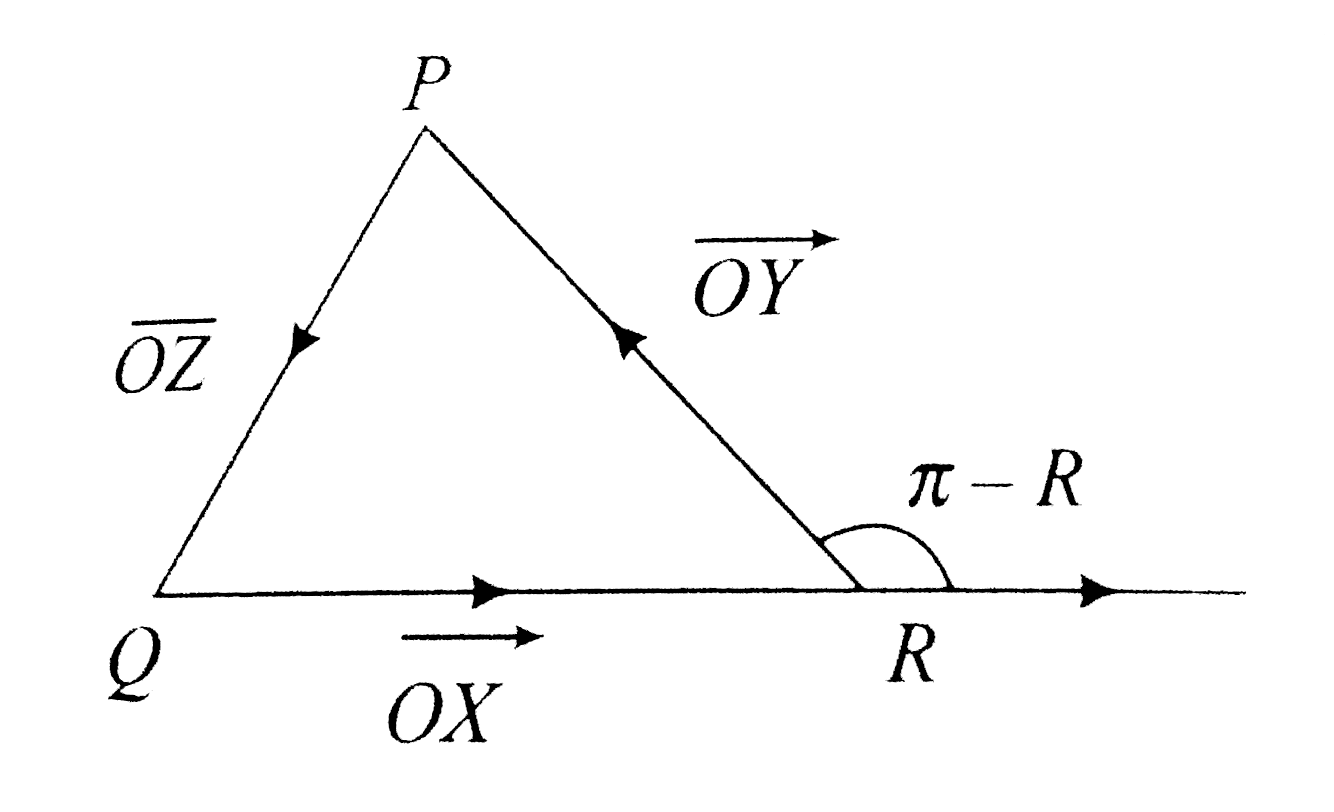
Class 12
MATHS
Let O be the origin, and O X x O Y ,...

Let `O` be the origin, and ` O X x O Y , O Z ` be three unit vectors in the direction of the sides ` Q R ` , ` R P ` , ` P Q ` , respectively of a triangle PQR. If the triangle PQR varies, then the minimum value of `cos(P+Q)+cos(Q+R)+cos(R+P)` is: `-3/2` (b) `5/3` (c) `3/2` (d) `-5/3`

A

`-(5)/(3)`

B

`-(3)/(2)`

C

`(3)/(2)`

D

`(5)/(3)`

Text Solution

Verified by Experts

The correct Answer is:
B
`-(cosP+cosQ+cosR)`
`= vec(OX).vec(OY)+vec(OZ)+vec(OZ).vec(OX)`
`=((vec(OX)+vec(OY)+vec(OZ))^(2)-(|vec(OX)|^(2)+|vec(OY)|^(2)+|vec(OZ)|^(2)))/(2) ge-(3)/(2)`
Promotional Banner

Topper's Solved these Questions

  • JEE 2019

    CENGAGE PUBLICATION|Exercise chapter -3|1 Videos

  • JEE 2019

    CENGAGE PUBLICATION|Exercise MCQ|92 Videos

  • JEE 2019

    CENGAGE PUBLICATION|Exercise chapter -2|1 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE PUBLICATION|Exercise All Questions|541 Videos

  • LIMITS

    CENGAGE PUBLICATION|Exercise Comprehension Type|4 Videos

Similar Questions

Explore conceptually related problems

Let p,q,r be the sides opposite to the angles P,Q,R respectively in a triangle PQR. Then 2prsin((P-Q+R)/2) equal

Let p,q,r be the sides opposite to the angles P,Q, R respectively in a triangle PQR if r^(2)sin P sin Q= pq , then the triangle is

Let p,q,r be the sides opposite to the angles P,Q, R respectively in a triangle PQR if 2prsin((P-Q+R)/(2)) equals

Let P(2 ,3), Q ( -2 ,1) be the vertices of the triangle PQR .If the centroid of trianglePQR lies on the line 2x + 3y =1 , them locus of R is

Let P (2 , -3) , Q (-2 , 1) be the vertices of the triangle PQR . If the centroid of Delta PQR lies on the line 2x + 3y = 1 , then the locus of R is _

If P,Q,R are angles of triangle PQR then the value of |{:(-1, cos R, cosQ),(cosR,-1,cosP),(cosQ, cosP,-1):}| is equal to

Let p,q,r be the altitudes of a triangle with area s and perimeter 2t. Then the value of 1/p+1/q+1/r is

Let P = (-1, 0), Q = (0, 0) and R = (3, 3sqrt3 ) be three points. The equation of the bisector of the angle PQR

O P Q R is a square and M ,N are the midpoints of the sides P Q and Q R , respectively. If the ratio of the area of the square to that of triangle O M N is lambda:6, then lambda/4 is equal to 2 (b) 4 (c) 2 (d) 16

Show that the points (p , q , r) , (q , r , p) and (r , p , q) are the vertices of an equilateral triangle.