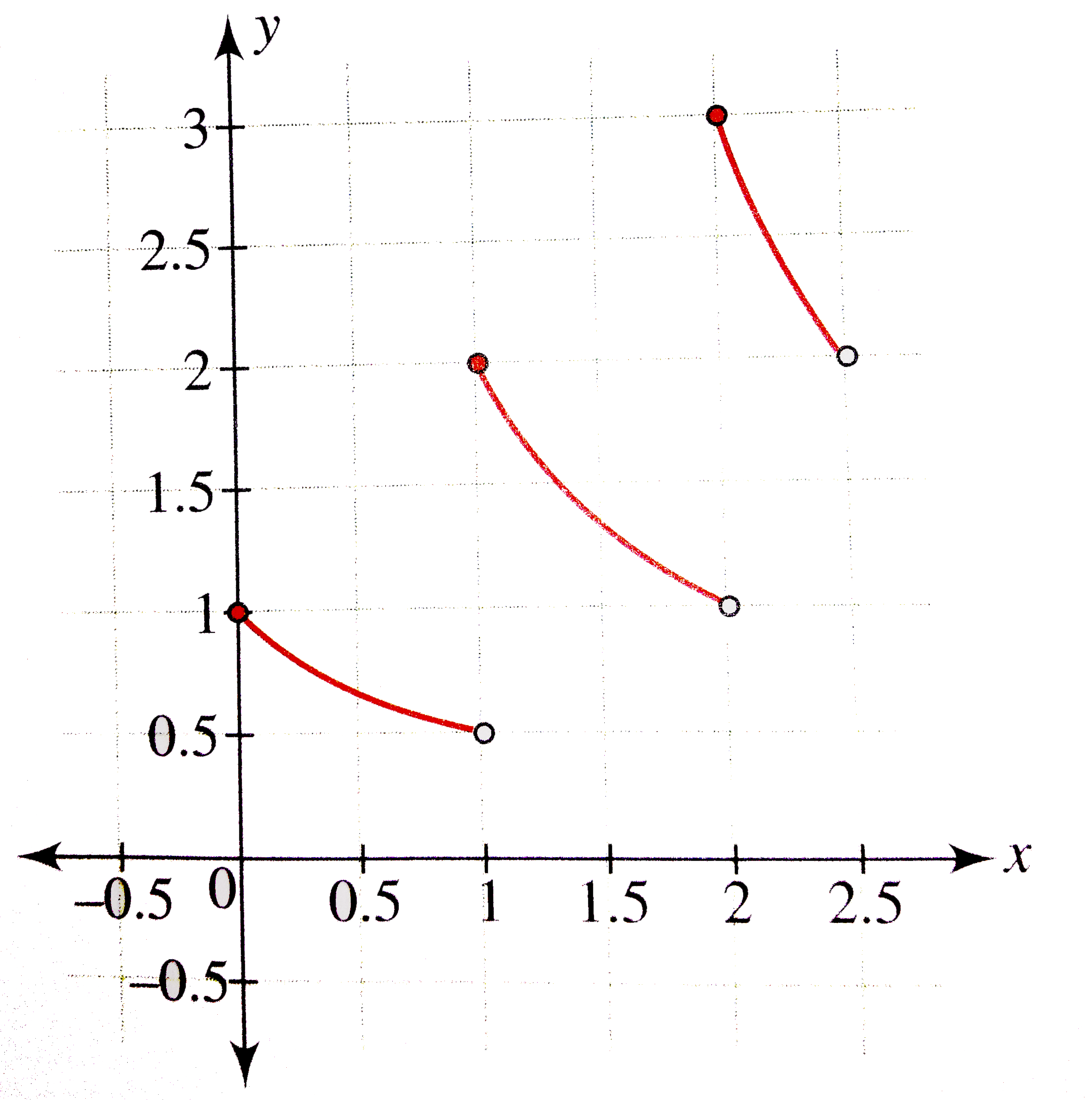
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-GRAPHS OF ELEMENTARY FUNCTIONS -EXERCISES
- Draw the graph of f(x) =y= |x-1|+3|x-2|-5|x-4| and find the values of ...
Text Solution
|
- Find the set of real value(s) of a for which the equation |2x+3|+2x-3|...
Text Solution
|
- Draw the graph of y= 2^(((|x|+x))/(x)).
Text Solution
|
- Draw the graph of y= x ^((1)/(log(e)x)).
Text Solution
|
- Find the number of solutions to the equation x+log(e)x=0.
Text Solution
|
- draw the graph of f(x)=x+[x], [.] denotes greatest integer function.
Text Solution
|
- Given f(x) is a periodic function with period 2 and it is defined as ...
Text Solution
|
- Draw the region of relation [x][y]= 6, x, y ge 0. Here [*] denotes the...
Text Solution
|
- lim(xrarrc)f(x) does not exist for wher [.] represent greatest integ...
Text Solution
|
- Let f(x) = ([x]+1)/({x}+1) for f: [0, (5)/(2) ) to ((1)/(2) , 3], whe...
Text Solution
|
- Draw the graph of y= 2^({x}), where {*} represents the fractional part...
Text Solution
|
- The area of the region containing the points (x , y) satisfying 4lt=x^...
Text Solution
|
- Draw the graph of y= -sqrt(x^(2)+2)
Text Solution
|
- Draw the graph of y=|x|^(1/2) for -1lt=x<1.
Text Solution
|
- Draw the graph of f(x) = "sgn"(log(0.5) x).
Text Solution
|
- The graph of y=f(x) is as shown in the following figure. Draw the grap...
Text Solution
|
- Discuss the continuity of f(x)=(lim)(n->oo)(x^(2n)-1)/(x^(2n)+1)
Text Solution
|
- An even periodic function f:R to R with period 4 is such that f(x)=...
Text Solution
|
- The function f(x) = "max"{(1-x), (1+x), 2}, x in (-oo, oo) is
Text Solution
|
- If f (x) = min { 1, x^2 , x^3} then
Text Solution
|