Home
Class 12
MATHS
Evaluate : [underset(x to 0)lim (sin x)/...

Evaluate : `[underset(x to 0)lim (sin x)/(x)]`, where `[*]` represents the greatest integer function.

Text Solution

Verified by Experts

See the graphs of y=x and `sin x` in the following figure.

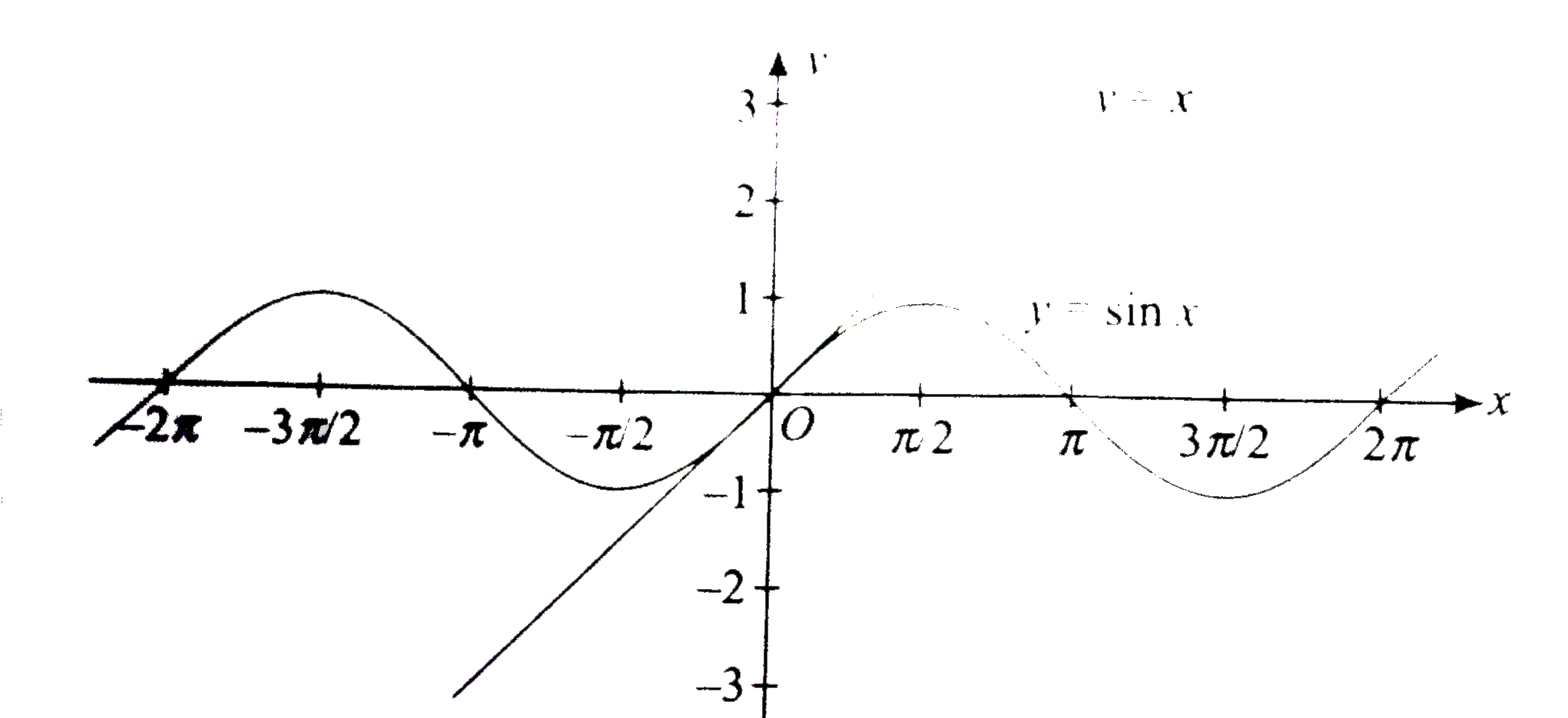
From the figure when `xto0^(+)`,graph of y=x is above the graph of `y=sinx`
i.e.,`" "sinxltx" or " (sinx)/(x)lt1`
`implies" "underset(xto0^(+))lim(sinx)/(x)=1^(1-)`
`implies" "[underset(xto0^(+))lim(sinx)/(x)]=0`
When `xto0^(-)`, graph of y=x is below the graph of `y=sinx`
i.e., `sinxltx" or " (sinx)/(x)lt1" "`(as x is negative)
`implies" "underset(xto0^(-))lim(sinx)/(x)=1^(-)`
`implies" "[underset(xto0^(-))lim(sinx)/(x)]=0`
Thus, `[underset(xto0^(-))lim(sinx)/(x)]=0`
Promotional Banner

Topper's Solved these Questions

  • LIMITS

    CENGAGE PUBLICATION|Exercise Solved Examples|15 Videos

  • LIMITS

    CENGAGE PUBLICATION|Exercise EXERCISE 2.1|10 Videos

  • JEE 2019

    CENGAGE PUBLICATION|Exercise Chapter 10|8 Videos

  • LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS

    CENGAGE PUBLICATION|Exercise DPP 1.2|10 Videos

Similar Questions

Explore conceptually related problems

Evaluate : [lim_(x to 0) (sin x)/(x)] , where [*] represents the greatest integer function.

Evaluate : [lim_(x to 0) (tan x)/(x)] , where [*] represents the greatest integer function.

Evalute [lim_(xto0) (sin^(-1)x)/(x)]=1 , where [*] represets the greatest interger function.

underset(xrarr0)(lim)[(sin^(-1)x)/(tan^(-1)x)]= (where [.] denotes the greatest integer function)

lim_(xto0) [(1-e^(x))(sinx)/(|x|)] is (where [.] represents the greatest integer function )

Evaluate : underset(x rarr 0)lim (sin(x^(2)-x))/x

Evaluate underset(xrarr0^(+))(lim)(x/a)[b/x] where [.] represents greatest integer function.

Draw the graph of |y|=[x] , where [.] represents the greatest integer function.

Evaluate : underset(xrarr0)"lim"(sin^(-1)x)/(2x)

Find x satisfying [tanx]+[cotx]=2, where [.] represents the greatest integer function.