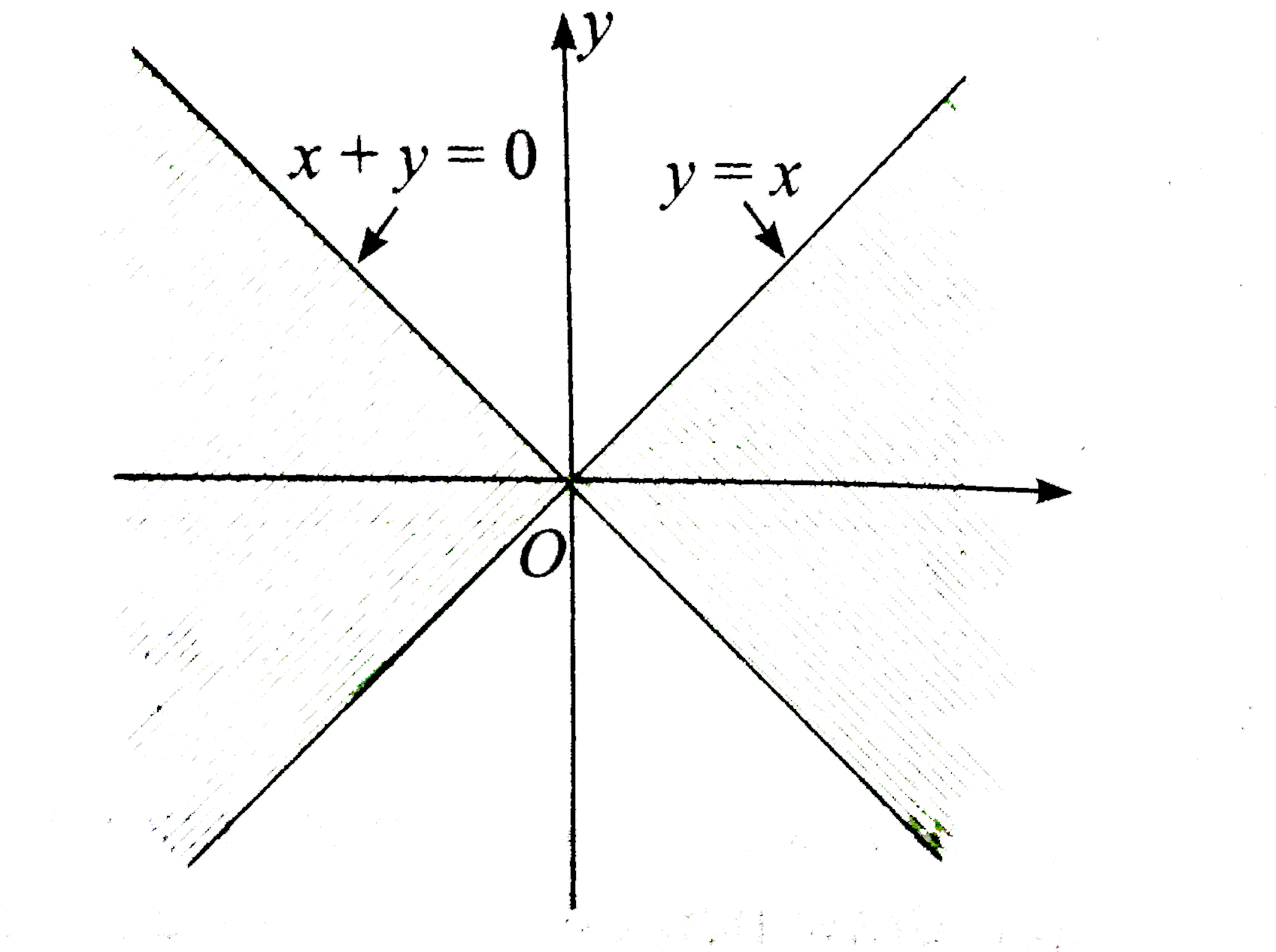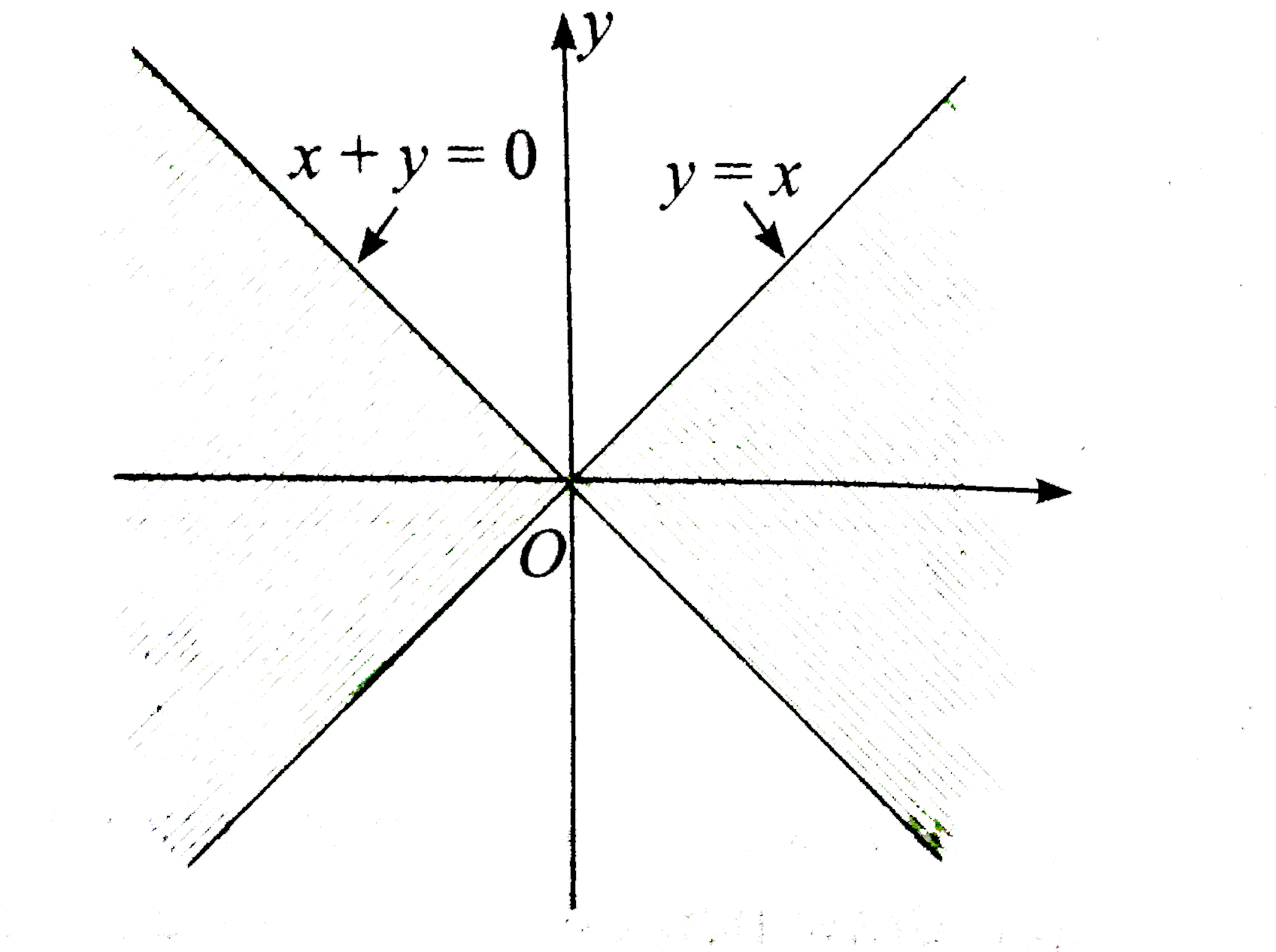`(i) |x+y| lt 2`
`therefore -2 lt x+y lt 2`
`rArr x+y+2 gt 0 and x+y-2 lt 0`
`L_(1)(x,y) = x+y+2 " and " L_(2)(x,y) = x+y-2`
`L_(1)(0,0) = 2 gt 0 " and" L_(2)(0,0) = -2 lt 0`
`" So ", x+y+2 gt 0` represents the region where origin lies and ` x+y-2 lt 0` also represents the region where origin lies.
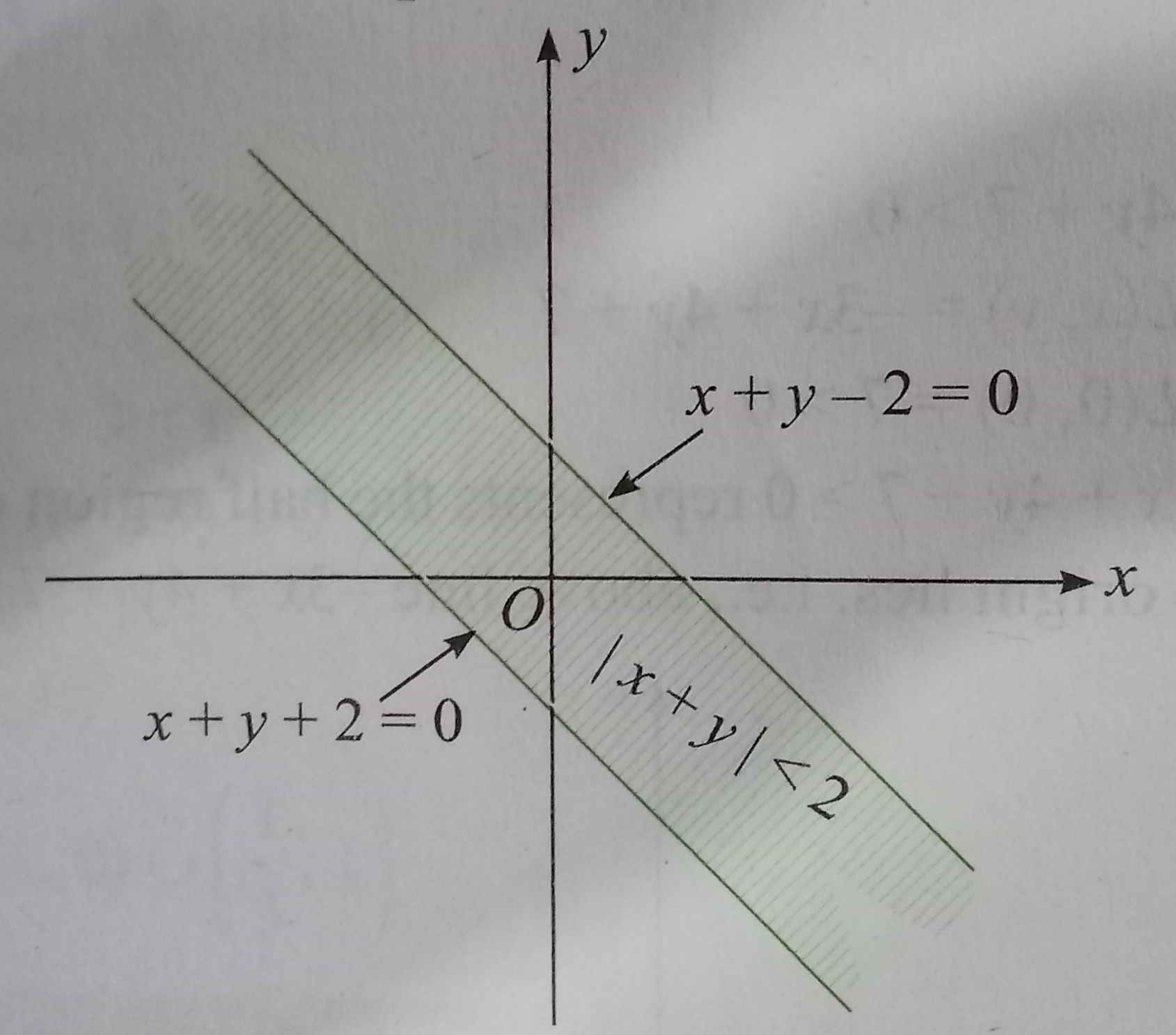
Thus, in general, `|ax + by +c| lt d` is the region of the points
between the lines ax+by+c =d and ax+by+c = -d.
`(ii) |2x-y| gt 3`
`therefore 2x-y lt-3 " and " 2x-y gt 3`
`rArr 2x-y+3 lt 0 " and " 2x-y-3 gt 0`
`L_(1) (x,y) = 2x-y+3 " and " L_(2) (x,y) = 2x-y-3`
`L_(1) (0,0) = 1 gt 0 " and " L_(2) (0,0) = -3 lt 0`
`" So, " 2x-y+3 lt 0` represents where origin doest not lie and `2x-y-3 gt 0` also represents the region where origin does not lie.
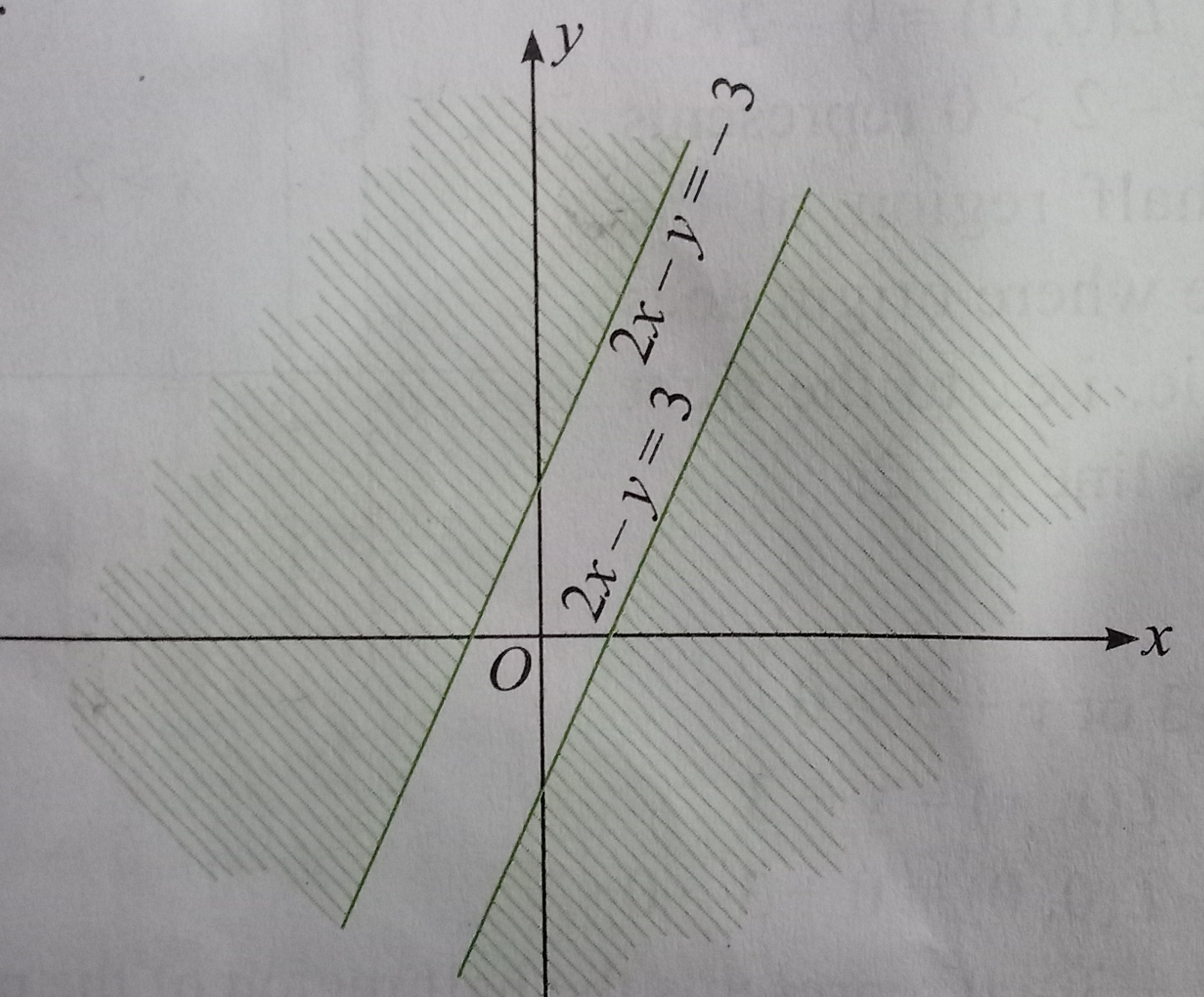
Thus, in general `|ax+by+c| gt d` is the region of the points which does not lie between the lines ax+by+c =d and ax+by+c=-d.
`(iii) |x| gt |y|`
` " If " x,y gt 0`, then we have `x gt y " or" x-y gt 0`.
Let L(x,y) = x-y.
`therefore L(1,0) = 1-0 gt 0.`
Hence, points satisfying this inequality lie below the line x-y=0 in first quadrant.

`" If" x gt 0, y gt 0`, then we have `x gt -y " or" x+y gt 0`.
Let L(x,y) = x+y.
`therefore L(1,0) = 1+0 gt 0`
Points satisfying this inequality lie above the line x+y=0 in fourth quadrant.
Similarly, we have one region in second quadrant and one in third quadant.
Combining all the cases, we have following region.