A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
STRAIGHT LINES
CENGAGE PUBLICATION|Exercise EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)|30 VideosSTRAIGHT LINES
CENGAGE PUBLICATION|Exercise EXERCISE (LINKED COMPREHENSION TYPE)|27 VideosSTRAIGHT LINES
CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 2.6|5 VideosSTRAIGHT LINE
CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|8 VideosTHEORY OF EQUATIONS
CENGAGE PUBLICATION|Exercise JEE ADVANCED (Numerical Value Type )|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-STRAIGHT LINES-EXERCISE (SINGLE CORRECT ANSWER TYPE)
- A variable line x/a + y/b = 1 moves in such a way that the harmonic me...
Text Solution
|
- Given A (0, 0) and B (x,y)with x epsilon (0,1) and y>0. Let the slope ...
Text Solution
|
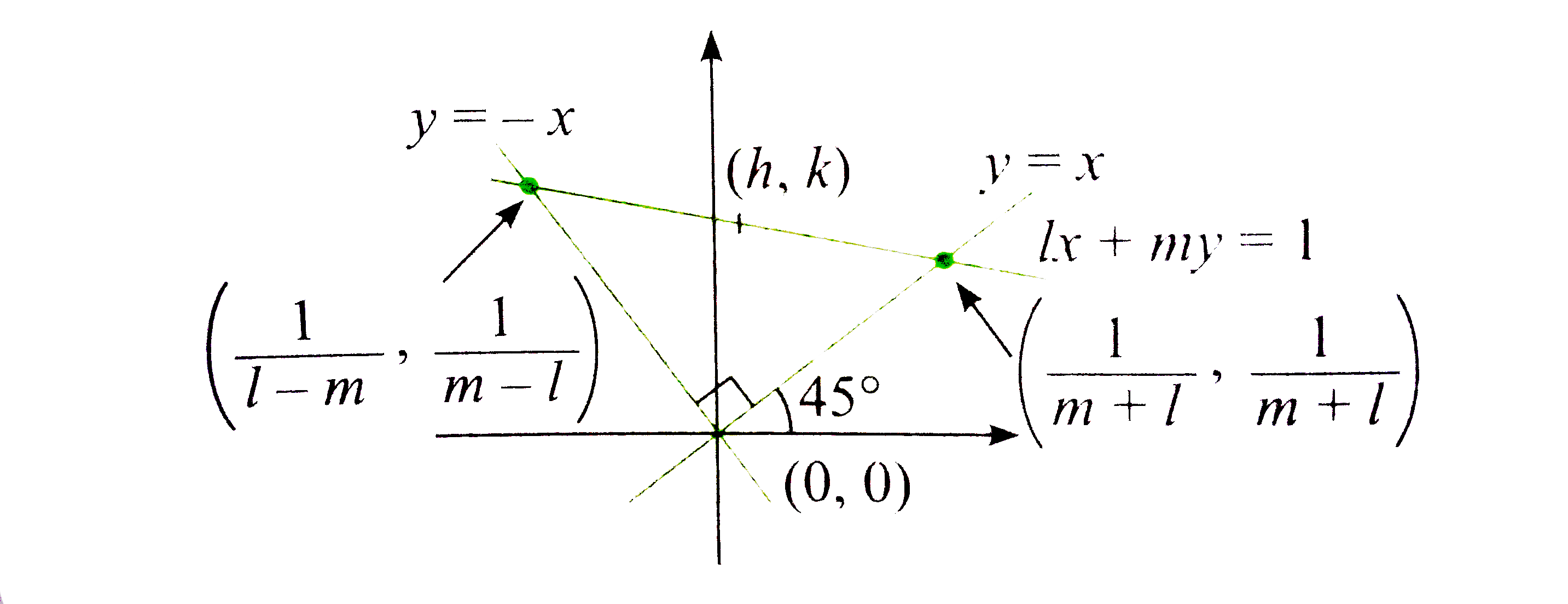
- A triangle is formed by the lines x+y=0,x-y=0, and l x+m y=1. If la n ...
Text Solution
|
- Let P be (5, 3) and a point R on y=x and Q on the x-axis be such that ...
Text Solution
|
- If a pair of perpendicular straight lines drawn through the origin f...
Text Solution
|
- A point P(x,y) moves that the sum of its distance from the lines 2x-y-...
Text Solution
|
- If AD, BE and CF are the altitudes of Delta ABC whose vertex A is (-4,...
Text Solution
|
- The vertex A of DeltaABC is (3,-1). The equation of median BE and angl...
Text Solution
|
- Suppose A, B are two points on 2x-y+3=0 and P(1,2) is such that PA=PB....
Text Solution
|
- Triangle formed by variable lines (a+b)x+(a-b)y-2ab=0 and (a-b)x+(a+b)...
Text Solution
|
- A light ray coming along the line 3x+4y=5 gets reflected from the line...
Text Solution
|
- The point (2,1) , translated parallel to the line x-y=3 by the distanc...
Text Solution
|
- If one diagonal of square is the portion of the line x/a+y/b=1intercep...
Text Solution
|
- The point P(2,1) is shifted through a distance 3sqrt(2) units measured...
Text Solution
|
- Let O be the origin. If A(1,0)a n dB(0,1)a n dP(x , y) are points such...
Text Solution
|
- In a triangle A B C , the bisectors of angles Ba n dC lies along the l...
Text Solution
|
- Line a x+b y+p=0 makes angle pi/4 with xcosalpha+ysinalpha=p ,p in R^...
Text Solution
|
- The equation of the line AB is y = x. If A and B lie on the same side ...
Text Solution
|
- The equation of the bisector of the acute angle between the lines 2x-y...
Text Solution
|
- The straight lines 4a x+3b y+c=0 passes through which point? , where a...
Text Solution
|