A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
STRAIGHT LINES
CENGAGE PUBLICATION|Exercise ARCHIVES (JEE ADVANCED)|3 VideosSTRAIGHT LINES
CENGAGE PUBLICATION|Exercise ARCHIVES (NUMERICAL VALUE TYPE)|1 VideosSTRAIGHT LINES
CENGAGE PUBLICATION|Exercise EXERCISE (NUMERICAL VALUE TYPE)|13 VideosSTRAIGHT LINE
CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|8 VideosTHEORY OF EQUATIONS
CENGAGE PUBLICATION|Exercise JEE ADVANCED (Numerical Value Type )|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-STRAIGHT LINES-ARCHIVES (JEE MAIN)
- The line L given by x/5 + y/b = 1 passes through the point (13,32).the...
Text Solution
|
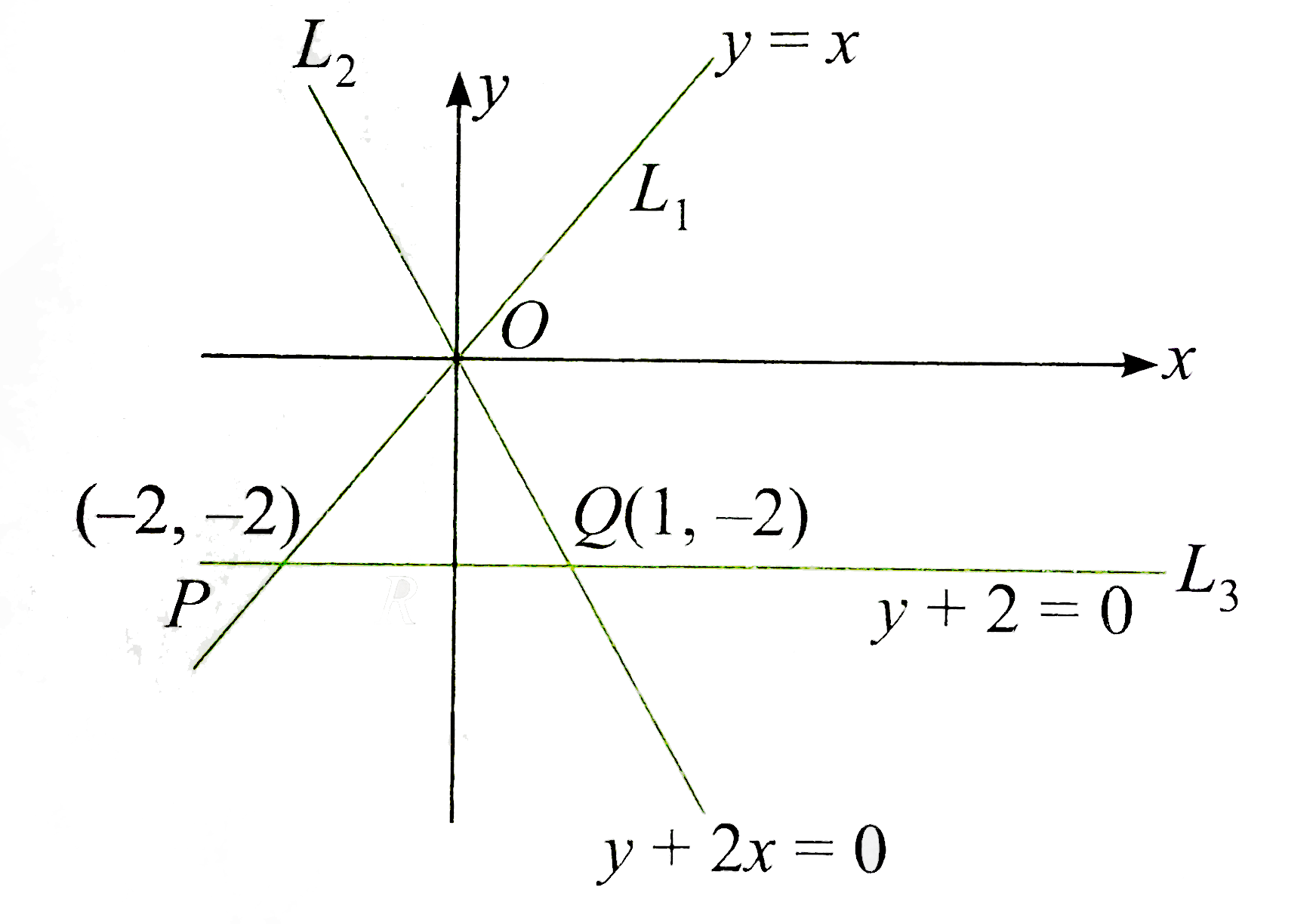
- The lines L1:y-x =0 and L2: 2x+y =0 intersect the line L3 : y+2 =0 at ...
Text Solution
|
- A line is drawn through the point ( 1, 2) to meet the coordinate axes ...
Text Solution
|
- The x-coordinate of the incentre of the triangle that has the coordi...
Text Solution
|
- A ray of light along x+sqrt(3)y=sqrt(3) gets reflected upon reaching x...
Text Solution
|
- Let a,b, c and d be non-zero numbers. If the point of intersection of...
Text Solution
|
- Let PS be the median of the triangle with vertices P(2,""2),""Q(6,-1)"...
Text Solution
|
- Locus of the image of the point (2, 3) in the line (2x-3y""+""4)""+"...
Text Solution
|
- Two sides of a rhombus are along the lines,x-y+1=0 and 7x-y-5=0 . If ...
Text Solution
|