Home
Class 12
MATHS
In A B C Prove that A B^2+A C^2=2(A O^2...

In ` A B C` Prove that `A B^2+A C^2=2(A O^2=2(A O^2+B O^2)` , where `O` is the middle point of `B C`

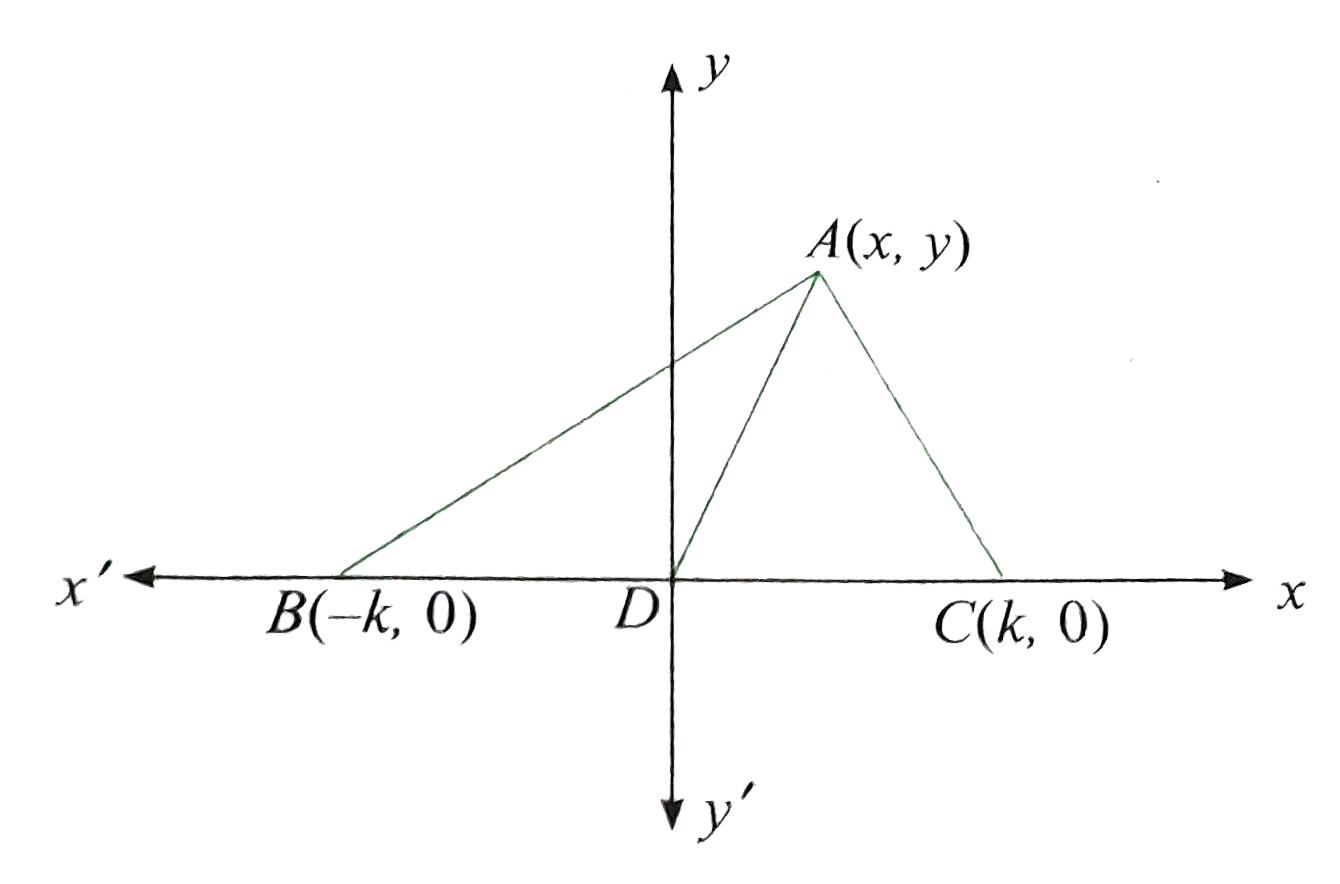
Text Solution

Verified by Experts

Let point B and C lie on the x-axis such that `BD=DC`, where, `D (0,0)` is midpoint of BC.
Let point A be (x,y).

`BD=k`.So, point B is `(-k,0)` and point C is `(k,0)`.
Now, `AB^2+AC^2=(x+k)^2+(y-0)^2+(x-k)^2+(y-0)^2`
`=x^2+k^2+2xk+y^2+x^2k^2-2xk+y^2`
`=2x^2+2y^2+2k^2=2(x^2+y^2+k^2)`
And `2(AD^2+BD^2)=2[(x-0)^2+(y-0)^2+k^2]`
`=2(x^2+y^2+k^2)`
Therefore, `AB^2+AC^2=2(AD^2+BD^2)`
Promotional Banner

Topper's Solved these Questions

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Illustration1.11|1 Videos

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Illustration1.12|1 Videos

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Illustration1.9|1 Videos

  • COORDINATE SYSTEM

    CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 Videos

  • CROSS PRODUCTS

    CENGAGE PUBLICATION|Exercise DPP 2.2|13 Videos

Similar Questions

Explore conceptually related problems

In A B C Prove that A B^2+A C^2=2(A O^2+B O^2) , where O is the middle point of B C

In A B C , prove that (a-b)^2cos^2C/2+(a+b)^2sin^2C/2=c^2dot

Prove that the resultant of two forces acting at point O and represented by vec O B and vec O C is given by 2 vec O D ,where D is the midpoint of BC.

If a,b,c are in GP, Prove that, a(b^2+c^2) =c(a^2+b^2)

if vec (AO) + vec (O B) = vec (B O) + vec (O C) ,than prove that B is the midpoint of AC .

If a,b, c are in GP, Prove that a^2, b^2 , c^2 are in GP.

if a:b = b:c prove that ((a+b)/(b+c))^2 = (a^2+b^2)/(b^2+c^2) .

In any /_\ABC ,prove that sin(B-C)/(sin(B+C))=(b^2-c^2)/(a^2)

In any /_\ A B C , prove that (b^2-c^2)cotA+(c^2-a^2)cotB+(c^2-b^2)cotC=0

Let A_r ,r=1,2,3, , be the points on the number line such that O A_1,O A_2,O A_3dot are in G P , where O is the origin, and the common ratio of the G P be a positive proper fraction. Let M , be the middle point of the line segment A_r A_(r+1.) Then the value of sum_(r=1)^ooO M_r is equal to (a) (O A_1(O S A_1-O A_2))/(2(O A_1+O A_2)) (b) (O A_1(O A_2+O A_1))/(2(O A_1-O A_2) (c) (O A_1)/(2(O A_1-O A_2)) (d) oo