Home
Class 12
MATHS
Find the locus of the point of intersect...

Find the locus of the point of intersection of lines `xcosalpha+ysinalpha=a` and `xsinalpha-ycosalpha=b(alpha` is a variable).

Text Solution

Verified by Experts

The correct Answer is:
`(1)/(x^2)+(1)/(y^2)=(4)/(p^2)`

The equation of the variable line is `xcosalpha+ysinalpha=p`
Here P is a constant and `alpha` is the parameter (variable),
Let the line in (1) cuts- x and y-axes at A and B respectively,
Putting `y=0` in (1) , we get `A-=(psecalpha,0)`
Putting `x=0` in (1) we get `B-=(0,pcosec alpha)`.
AB is the portion of (1) intercepted between the axes.
Let P(h,k) be the midpoint of AB. we have to find the locus of pont (h,k) for this, we will to eliminate `alpha` and find a relation in h and k. Therefore.
`h=(psecalpha+0)/(2)=(p)/(2)secalpha" "(2)`
and `k=(0+pcosecalpha)/(2)=(p)/(2)cosec alpha`
From (2) , we get
`cosalpha=(p)/(2h)`
From (3)we get
`sinalpha=(p)/(2k)`
or `cos^2alpha+sin^2alpha=(p^2)/(4h^2)+(p^2)/(4k^2)`
or `(1)/(h^2)+(1)/(k^2)=(4)/(p^2)`
Hence,the locus of pont P(h,k) is `(1)/(x^2)+(1)/(y^2)=(4)/(p^2)`.
Promotional Banner

Topper's Solved these Questions

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Exercises|59 Videos

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Multiple correct|13 Videos

  • COORDINATE SYSYEM

    CENGAGE PUBLICATION|Exercise Concept applications 1.5|5 Videos

  • COORDINATE SYSTEM

    CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 Videos

  • CROSS PRODUCTS

    CENGAGE PUBLICATION|Exercise DPP 2.2|13 Videos

Similar Questions

Explore conceptually related problems

Show that the locus of the point of intersection of the lines x cos alpha + y sin alpha = a and x sin alpha - y cos alpha = a , when alpha varies, is a circle.

If theta is a variable and a is contant , then find the locus of the point of intersection of the lines xcostheta+ysintheta=aand xsintheta-ycostheta=a .

Prove that for all values of theta , the locus of the point of intersection of the lines xcostheta+ysintheta=a and xsintheta-ycostheta=b is a circle.

Show that the locus of the pt of intersection of the st.lines xcostheta+ysintheta=a and xsintheta-ycostheta=b is a circle.

If theta is a variable and a,b are constants then find the locus of the point of intersection of the lines xsintheta+ycostheta=aandxcostheta-ysintheta=b .

Find the locus of the mid-point of the portion of the line x cosalpha+ysinalpha=4 intercepted between the axes of coordinates.

For the variable t, the locus of the points of intersection of lines x-2y=t and x+2y=(1)/(t) is

Find the locus of the mid - point of the portion of the line x cos alpha + y sin alpha = 4 intercepted between the axes of coordinates .

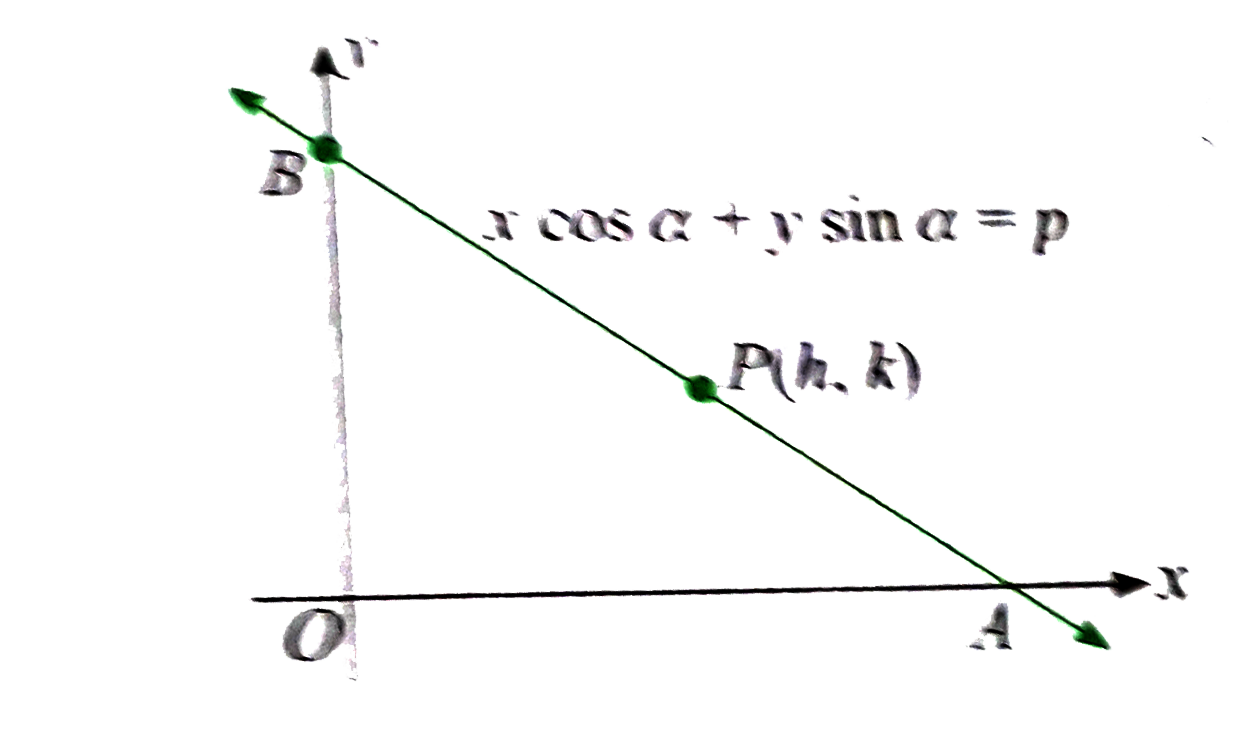
Find the locus of the middle point of the portion of the line xcosalpha+ysinalpha=p which is intercepted between the axes, given that p remains constant.

Show that the sum of the squares of the perpendiculars from the origin upon the lines xcosalpha+ysinalpha=acos2alphaandxsecalpha+ycossecalpha=2a is independent of alpha .