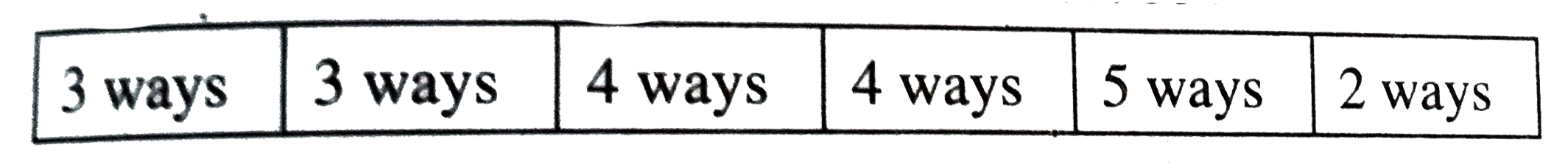A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PERMUTATION AND COMBINATION
CENGAGE PUBLICATION|Exercise Multiple Correct Answer|2 VideosPERMUTATION AND COMBINATION
CENGAGE PUBLICATION|Exercise Comprehension|8 VideosPARABOLA
CENGAGE PUBLICATION|Exercise Matching Column Type|1 VideosPRINCIPLE OF MATHEMATICAL INDUCTION
CENGAGE PUBLICATION|Exercise Sovled Examples|22 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-PERMUTATION AND COMBINATION-Comprehension
- How many six-digit numbers are there in which no digit is repeated, ev...
Text Solution
|
- Given are six 0's, five 1's and four 2's . Consider all possible perm...
Text Solution
|
- Given are six 0's, five 1's and four 2's . Consider all possible perm...
Text Solution
|
- The are 8 events that can be schedules in a week, then The total nu...
Text Solution
|
- The are 8 events that can be schedules in a week, then The total nu...
Text Solution
|
- The are 8 events that can be schedules in a week, then The total nu...
Text Solution
|
- Let a(1), a(2),…. and b(1),b(2),…. be arithemetic progression such tha...
Text Solution
|
- Let theta=(a(1),a(2),a(3),...,a(n)) be a given arrangement of n distin...
Text Solution
|
- There are 5 different colour balls and 5 boxes of colours same as thos...
Text Solution
|