Home
Class 12
MATHS
If the area of bounded between the x-axi...

If the area of bounded between the x-axis and the graph of `y=6x-3x^2` between the ordinates `x=1a n dx=a` is `19` units, then `a` can take the value `4or-2` two value are in (2,3) and one in `(-1,0)` two value are in (3,4) and one in `(-2,-1)` none of these

Text Solution

Verified by Experts

We have `y=3x(2-x)`

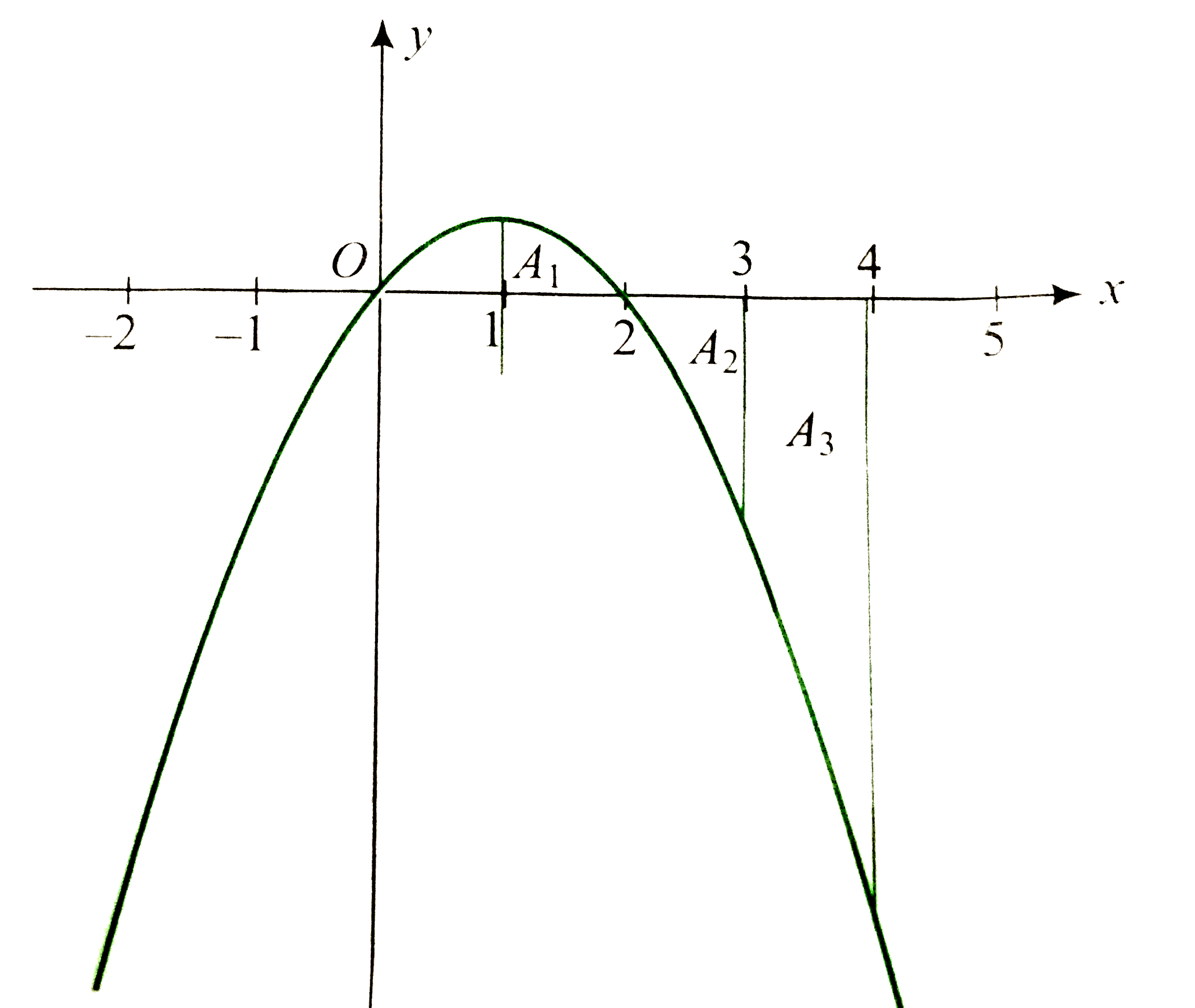
Graph of the function is downward parabola intersecting x-axis at `x=0 and x=2.`
`"Now "I=int(6x-3x^(2))dx=(6x^(2))/(2)-(3x^(3))/(3)`
`3x^(2)-x^(3)`
`x^(2)(3-x)=F(x)`
`"Now "A_(1)=F(2)-F(1)=4-2=2 "sq. units"`
`A_(2)=F(2)-F(3)=4-0=4 " sq. units"`
`A_(3)=F(3)-F(4)=0-(-16)=16 " sq. units"`
`"Since "A_(1)+A_(2)+A_(3)=22" sq. units."`
`So, a in (3,4)`
From the symmetric of the parabola, other value of lies in `(-2,-1)`
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE PUBLICATION|Exercise Solved Examples|10 Videos

  • AREA

    CENGAGE PUBLICATION|Exercise Concept Application Exercise 9.1|9 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE PUBLICATION|Exercise Subjective Type|2 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

Similar Questions

Explore conceptually related problems

If the area of bounded between the x-axis and the graph of y=6x-3x^2 between the ordinates x=1 and x=a is 19 units, then a can take the value: (A) 4 or -2 (B) one value is in (2, 3) and one in (-1, 0) (C) one value is in (3, 4) and one in (-2,-1) (D) none of these

Find the area bounded by the curve y^(2) = 4x the x-axis and the ordinate at x=4

Find the area bounded by the curve y=(x-1)(x-2)(x-3) lying between the ordinates x=0a n dx=3.

Find the area bounded by the curve y=(x-1)(x-2)(x-3) lying between the ordinates x=0a n dx=3.

The area bounded by the curves y=cosx and y=sinx between the ordinates x=0 and x=(3pi)/2 is

Find the area bounded by the x-axis, part of the curve y=(1+8/(x^2)) , and the ordinates at x=2a n dx=4. If the ordinate at x=a divides the area into two equal parts, then find adot

Area bounded by the curve y=x^(3) , the x-axis and the ordinates x = -2 and x = 1 is

The area (in square unit ) bounded by the curve y= sinx between the ordinates x=0, x= pi and the x -axis is-

The area (in square unit) bounded by the curve y= sin x, x-axis and the two ordinates x = pi ,x =2pi is-