Home
Class 12
MATHS
Prove that area common to ellipse (x^2)/...

Prove that area common to ellipse `(x^2)/(a^2)+(y^2)/(b^2)=1` and its auxiliary circle `x^2+y^2=a^2` is equal to the area of another ellipse of semi-axis a and a-b.

Text Solution

Verified by Experts

We have ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1.`
`therefore" "y=pmbsqrt(1-(x^(2))/(a^(2)))`

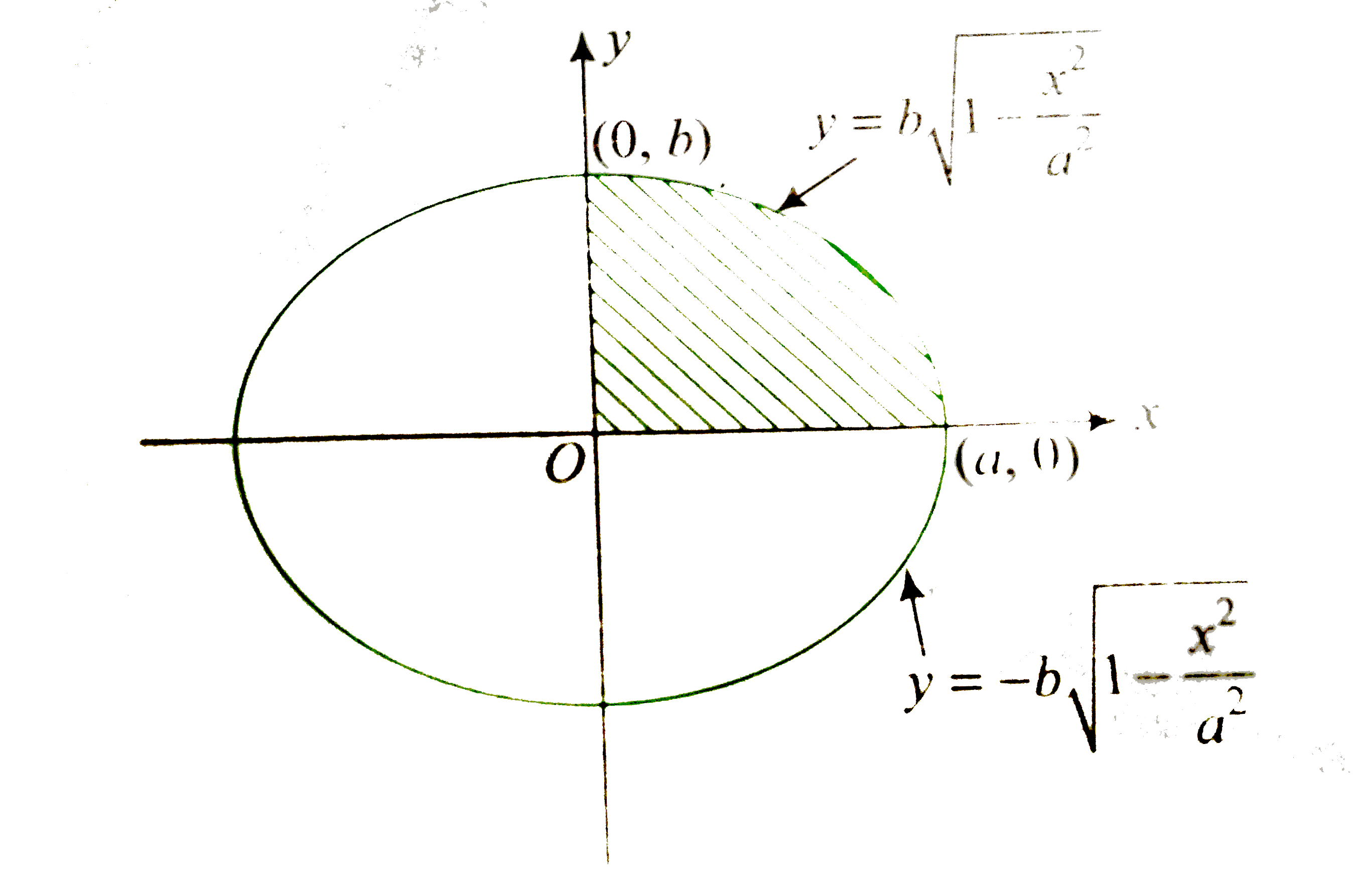
Since graph of the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` is symmetrical about both the axis,
Area enclosed by ellipse `=4xx` Area in the first quadrant
`=4xx overset(a)underset(0)intbsqrt(-1(x^(2))/(a^(2)))dx`
`=(4b)/(a)overset(a)underset(0)intsqrt(a^(2)-x^(2))dx`
`=(4b)/(a)[(x)/(2)sqrt(a^(2)-x^(2))+(a^(2))/(2)sin^(-1)""(x)/(a)]_(0)^(a)`
`=(4b)/(a)[0+(a^(2))/(2)sin^(-1)1-0-0]`
`=(4b)/(2)[(a^(2))/(2)cdot(pi)/(2)]`
`=pi ab`
In the following figure ellipse and its auxiliary are drawn.
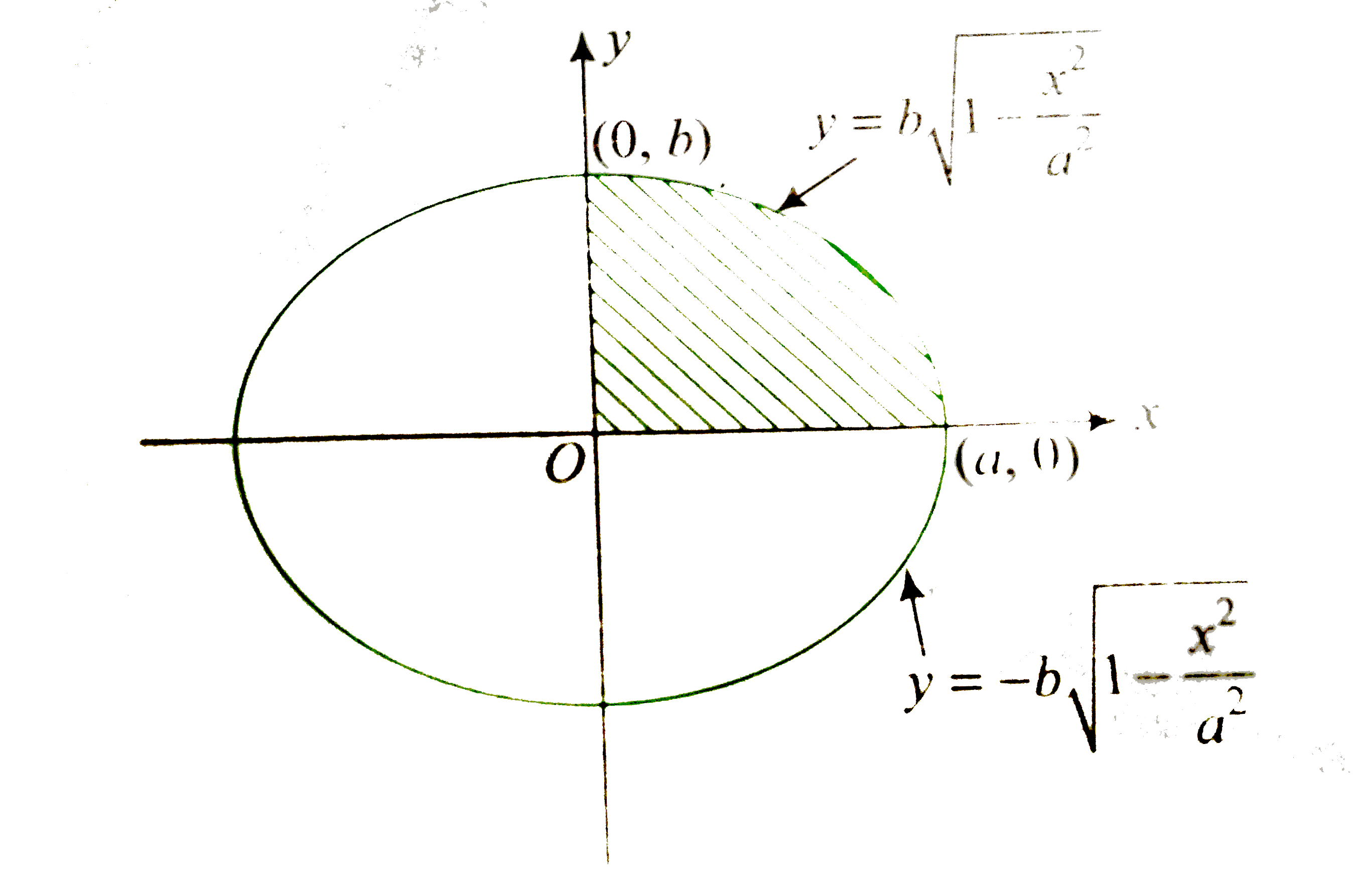
ltbvrgt Area of the ellipse `=pi ab`
Area of the circle `=pia^(2)`
Common area between curves is that shown as shaded region
=Area of circle - area of ellipse
`=piab-pia^(2)`
`=pia(b-a)`
This is area of the ellipse whose semi axis are a and (a-b).
One of the possible equations of ellipse is `(x^(2))/(2)+(y^(2))/((a-b)^(2))=1`
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE PUBLICATION|Exercise Solved Examples|10 Videos

  • AREA

    CENGAGE PUBLICATION|Exercise Concept Application Exercise 9.1|9 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE PUBLICATION|Exercise Subjective Type|2 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

Similar Questions

Explore conceptually related problems

Find the maximum area of the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 which touches the line y=3x+2.

Find the slope of a common tangent to the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 and a concentric circle of radius rdot

If the area of the ellipse ((x^2)/(a^2))+((y^2)/(b^2))=1 is 4pi , then find the maximum area of rectangle inscribed in the ellipse.

Tangents are drawn to the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1,(a > b), and the circle x^2+y^2=a^2 at the points where a common ordinate cuts them (on the same side of the x-axis). Then the greatest acute angle between these tangents is given by (A) tan^(-1)((a-b)/(2sqrt(a b))) (B) tan^(-1)((a+b)/(2sqrt(a b))) (C) tan^(-1)((2a b)/(sqrt(a-b))) (D) tan^(-1)((2a b)/(sqrt(a+b)))

The parametric equations of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)) = 1 are _

Prove that the chord of contact of the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 with respect to any point on the directrix is a focal chord.

If any tangent to the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 intercepts equal lengths l on the axes, then find l .

P is a variable on the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 with A A ' as the major axis. Find the maximum area of triangle A P A '

Calculated the area enclosed by the ellipse 4x^(2) +9y^(2) =36 and the x-axis

The tangent at the point theta on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 , meets its auxiliary circle at two points whose join subtends a right angle at the centre, show that the eccentricity of the ellipse is given by, (1)/(e^(2))=1+sin^(2)theta