`y= e^(x) and y= log_(e)x` are inverse to each other.
So, their graphs are symmetrical about the line y=x.
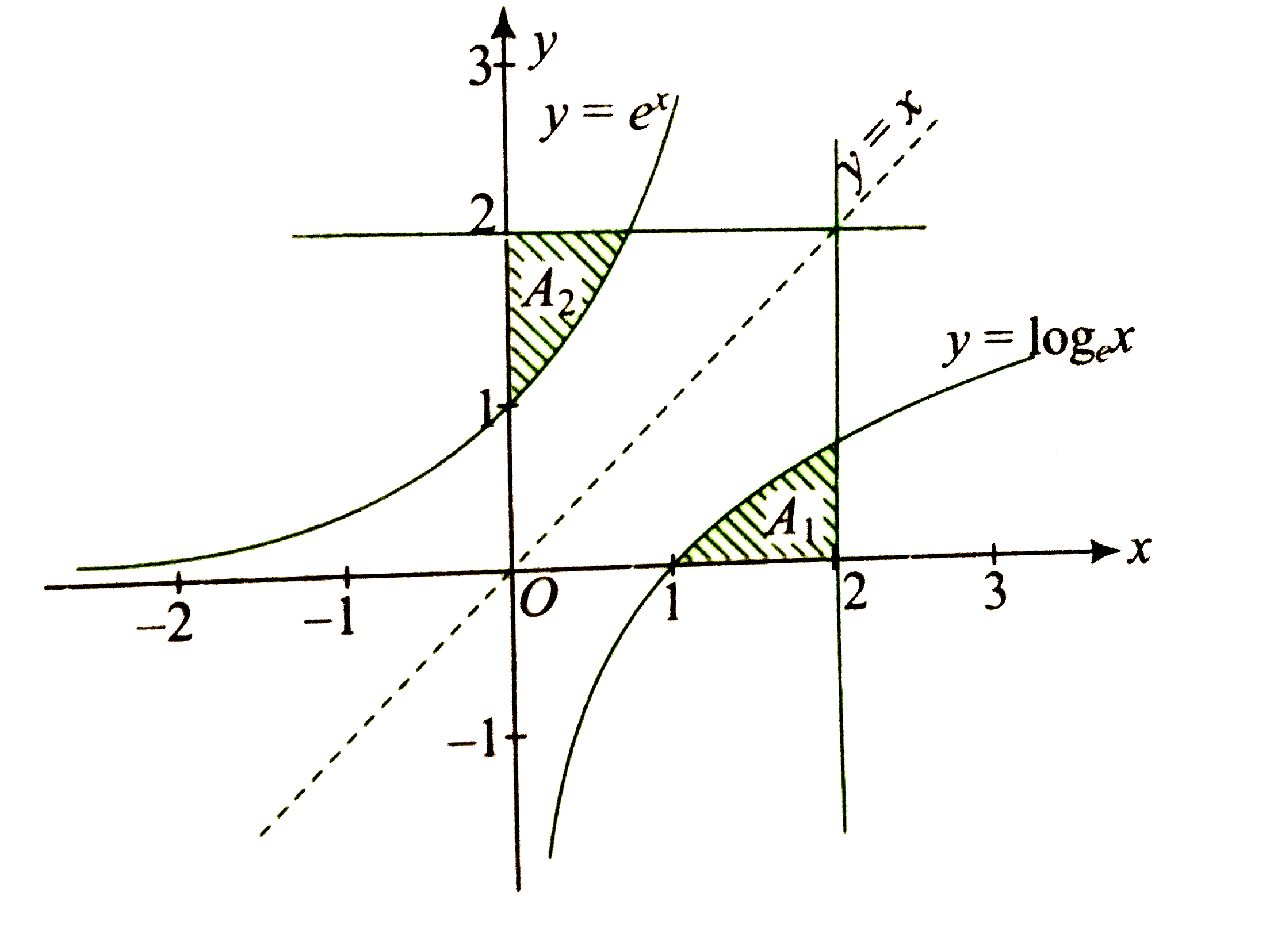
Area of the square OABC is 4 sq. units.
Areas `A_(1) and A_(2)` are same.
So, area of the shaded region `=2A_(1)`
`=2overset(2)underset(1)intlog_(e) xdx`
`=2[x log_(e) x -x ]_(1)^(2)`
`=2[2 log_(e)2-1]` sq. unit
Therefore, the area of the unshaded region of the square
`=4-2[2 log_(e)2-1]=(6-4 log_(e)2)` sq. units