Find the area bounded by the curve `y=(x-1)(x-2)(x-3)` lying between the ordinates `x=0a n dx=3.`

Explanation

`y=f(x)=(x-1) (x-2)(x-3)`
`y=0," then "x=1, 2, 3.`
So, graph of the function is as shown in the following figure.

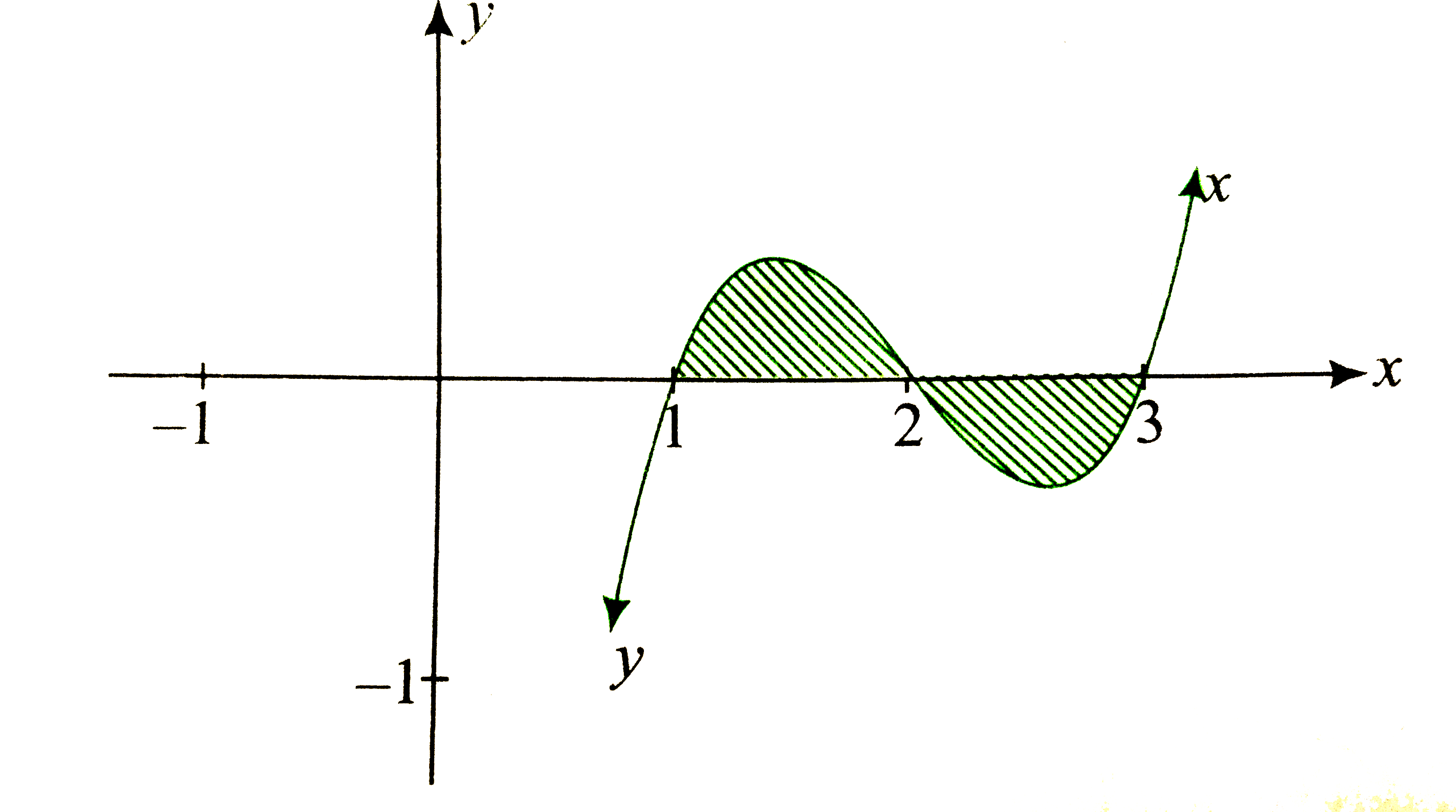
`"Since "f(2-x)=-f(2+x)`
`overset(2)underset(1)intf(x)dx=|underset(2)overset(3)intf(x)dx|`
`therefore" Area of the shaded region,"`
`A=2underset(1)overset(2)intf(x^(3)-6x^(2)+11x-6)dx`
`=2[(x^(4))/(4)-2x^(3)+(11x^(2))/(2)-6x]_(1)^(2)`
`=2xx(1)/(4)=(1)/(2)`