Find the area bounded by `y=sin^(-1)x ,y=cos^(-1)x` ,and the `X`-axis.

Explanation

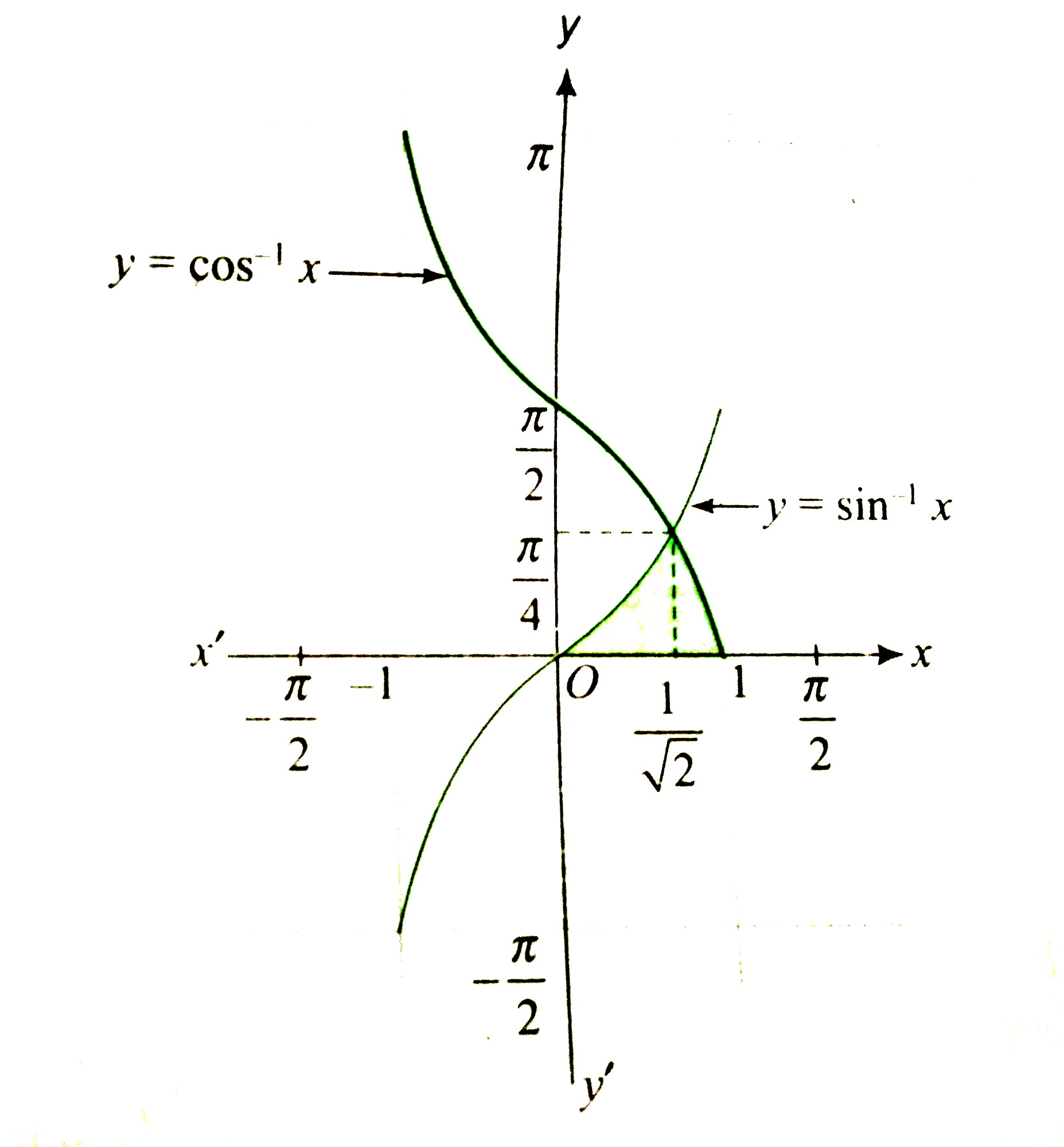
We have to find the area bounded by `y=sin^(-1)x, y=cos^(-1)x,` and the x-axis. If integration along x-axis is used then
`A=overset(1//sqrt(2))underset(0)intsin^(-1)x dx +overset(1)underset(1sqrt(2))intcos^(-1) x dx`
If integration along y-axis is used, then
`A=overset(pi//4)underset(0)int(cos y- sin y)dy`
`=[sin y +cos y]_(0)^(pi//4)`
`=[(1)/(sqrt(2))+(1)/(sqrt(2))-1]`
`=sqrt(2)-1`