A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
AREA
CENGAGE PUBLICATION|Exercise Single Correct Answer Type|30 VideosAREA
CENGAGE PUBLICATION|Exercise Multiple Correct Answer Type|3 VideosAREA
CENGAGE PUBLICATION|Exercise Numerical Value Type|18 VideosAPPLICATIONS OF DERIVATIVES
CENGAGE PUBLICATION|Exercise Subjective Type|2 VideosBINOMIAL THEOREM
CENGAGE PUBLICATION|Exercise Comprehension|11 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-AREA-Archives
- The area of the figure bounded by the parabola (y-2)^2=x-1, the tangen...
Text Solution
|
- The area bounded by the curves y=cosx and y=sinx between the ordinates...
Text Solution
|
- The area of the region enclosed by the curve y=x, x=e,y=1/x and the po...
Text Solution
|
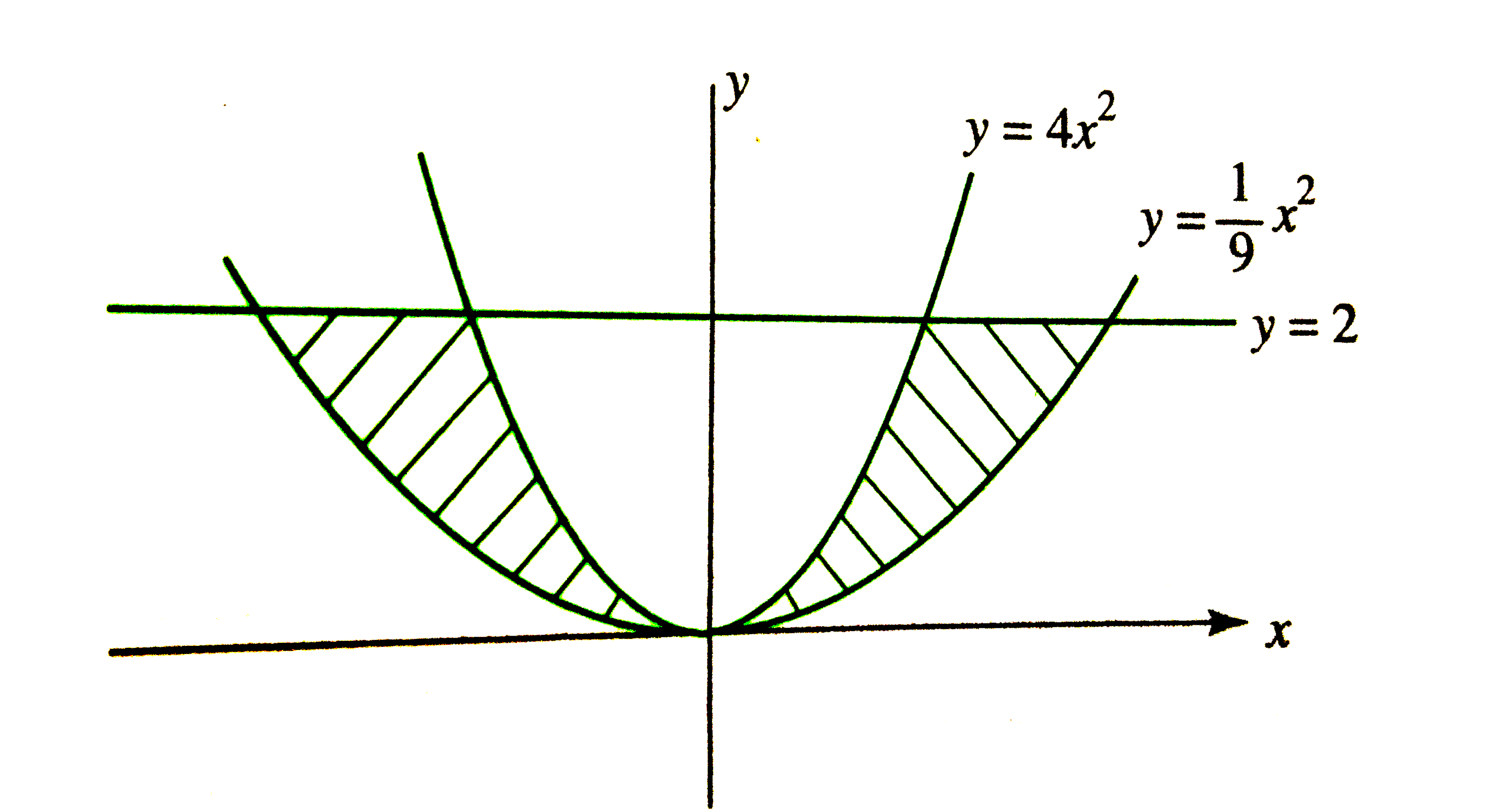
- The area bounded by the parabolas y=4x^(2), y=(x^(2))/(9) and the stra...
Text Solution
|
- The area bounded by the curves y=sqrt(x),2y+3=x , and x-axis in the 1s...
Text Solution
|
- The area of the region described by A = {(x,y) : x^2 + y^2 lt= 1and y^...
Text Solution
|
- The area (in sq. units) of the region described by {x,y):y^(2)le2x and...
Text Solution
|
- The area (in sq units) of the region {(x, y) : y^2 gt= 2x and x^2 + y^...
Text Solution
|
- The area (in sq units) of the region bounded by the curve y = sqrtx an...
Text Solution
|
- Let g(x)=cos^2 x,f(x)=sqrtx and alpha,beta (alpha < beta) be the roo...
Text Solution
|